Section : Prédiction pour un processus
Précédent : Fonction de prévision
Suivant : Exercice 8.
Notons
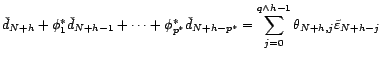 . On a
la formule de récurrence
. On a
la formule de récurrence
Exemples :
Par récurrence, on montre ainsi qu'il existe des
coefficients
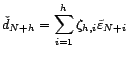 tels que
L'erreur de prévision est donc égale à
Le calcul des coefficients
tels que
L'erreur de prévision est donc égale à
Le calcul des coefficients
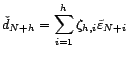 s'effectue grâce
à la formule de récurrence
avec
s'effectue grâce
à la formule de récurrence
avec
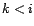 si
si 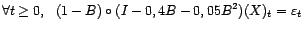 .
.
Thierry Cabanal-Duvillard
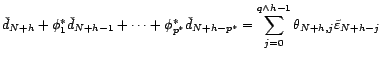 . On a
la formule de récurrence
. On a
la formule de récurrence
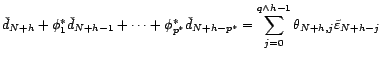 . On a
la formule de récurrence
. On a
la formule de récurrence
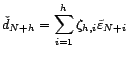 tels que
tels que
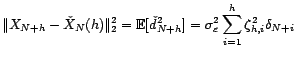
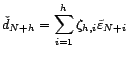 s'effectue grâce
à la formule de récurrence
s'effectue grâce
à la formule de récurrence