Section : Prédiction pour un processus
Précédent : Prédiction pour un processus
Suivant : Erreur
de prévision
La suite
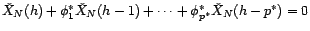 vérifie la
relation de récurrence
vérifie la
relation de récurrence
qui admet comme polynôme caractéristique
Les racines de ce polynôme sont
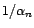 ,...,
,...,
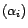 avec
avec
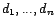 les racines de
les racines de
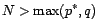 . Soient
. Soient
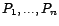 les multiplicités
respectives de ces racines. Alors il existe
les multiplicités
respectives de ces racines. Alors il existe
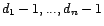 , polynômes de
degrés respectifs
, polynômes de
degrés respectifs
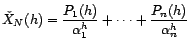 tels que, pour tout
tels que, pour tout 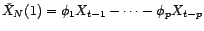 ,
Les valeurs initiales
,
Les valeurs initiales
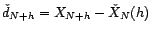 qui
permettent de déterminer
qui
permettent de déterminer
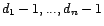 , sont appelées
valeurs pivotales.
, sont appelées
valeurs pivotales.
Thierry Cabanal-Duvillard
![]() vérifie la
relation de récurrence
vérifie la
relation de récurrence