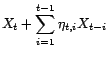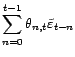Section : Prédiction pour un processus
Précédent : Exercice 6.
Suivant : Prédiction pour un processus
Soit  un processus faiblement stationnaire de
type MA(1), vérifiant :
avec
un processus faiblement stationnaire de
type MA(1), vérifiant :
avec
 bruit blanc faible de variance
1. On définit, à l'aide de l'algorithme des
innovations, les variables aléatoires
bruit blanc faible de variance
1. On définit, à l'aide de l'algorithme des
innovations, les variables aléatoires
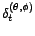 et les coefficients
et les coefficients
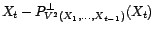 tels
que
tels
que
- Que vaut
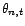 ? Que valent
? Que valent
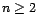 pour
pour 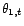 ? Quelle est la limite de
? Quelle est la limite de
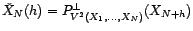 , quand
, quand 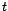 tend vers l'infini ?
tend vers l'infini ?
- Déterminer en fonction de
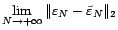 et de
et de
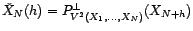 les prédicteurs
linéaires
les prédicteurs
linéaires
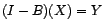 , ainsi que
la variance des erreurs de prédiction. En donner une
approximation pour
, ainsi que
la variance des erreurs de prédiction. En donner une
approximation pour 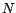 grand.
grand.
Thierry Cabanal-Duvillard