Section : Modèles ARIMA
Précédent : Suppression d'une tendance polynômiale
Suivant : Choix
d'un modèle ARIMA
Une dérivation par 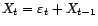 est aussi
utile pour étudier des processus non stationnaires qui
n'admettent pas pour autant de tendance simple.
est aussi
utile pour étudier des processus non stationnaires qui
n'admettent pas pour autant de tendance simple.
Exemple : cas d'une marche aléatoire 
avec
 bruit blanc. Alors le processus
dérivé
bruit blanc. Alors le processus
dérivé
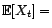 est égal en fait à
est égal en fait à
 , et il est facile de
l'identifier. D'autre part, on vérifie facilement que
, et il est facile de
l'identifier. D'autre part, on vérifie facilement que
![$ {\mathbb{E}}[X_t]=$](img1457.gif) cte, et qu'il ne
présente donc pas de tendance particulière.
cte, et qu'il ne
présente donc pas de tendance particulière.
Figure: Graphe d'une
réalisation de la marche aléatoire  pour
pour
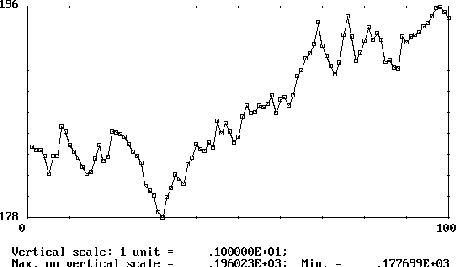
|
|
Figure:
Autocorrélogramme associé
|
|
Il peut être utile aussi de dériver pour obtenir
une meilleure précision des paramètres du
modèle. Supposons que l'on ait une série temporelle
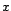 que l'on modélise par un processus
ARMA vérifiant
que l'on modélise par un processus
ARMA vérifiant
avec 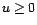 un polynôme possédant
une racine proche de l'unité. Dans ce cas, l'intervalle de
confiance pour l'estimation des coefficients de
un polynôme possédant
une racine proche de l'unité. Dans ce cas, l'intervalle de
confiance pour l'estimation des coefficients de 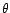 et
et 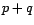 sera grand. La raison
en est que le processus
sera grand. La raison
en est que le processus  est très proche d'un
processus non stationnaire, et sur l'intervalle de temps fini sur
lequel on le considère, il peut même en être
quasi indiscernable. Or les résultats de convergence des
estimations ne sont valables que pour des processus stationnaires.
est très proche d'un
processus non stationnaire, et sur l'intervalle de temps fini sur
lequel on le considère, il peut même en être
quasi indiscernable. Or les résultats de convergence des
estimations ne sont valables que pour des processus stationnaires.
Dans cette situation, il peut être
préférable de dériver 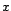 par
par
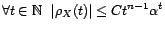 , et de modéliser la
série résultante par un processus ARMA dont le
polynôme
, et de modéliser la
série résultante par un processus ARMA dont le
polynôme 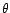 associé ne
possède pas de racine proche de l'unité, et pour
lequel l'approximation des autres coefficients sera plus fine.
associé ne
possède pas de racine proche de l'unité, et pour
lequel l'approximation des autres coefficients sera plus fine.
Les situations où il est utile de dériver sont
donc plus nombreuses que celles où il s'agit simplement
d'enlever une tendance polynômiale. Mais dans le cas
où une tendance est présente qu'il s'agit de
soustraire, notons que si la dérivation peut permettre de
modéliser correctement la série temporelle, en
revanche elle ne donne pas d'information sur la tendance
elle-même.
Section : Modèles ARIMA
Précédent : Suppression d'une tendance polynômiale
Suivant : Choix
d'un modèle ARIMA
Thierry Cabanal-Duvillard
![]()
![]() que l'on modélise par un processus
ARMA vérifiant
que l'on modélise par un processus
ARMA vérifiant
![]() par
par
![]() , et de modéliser la
série résultante par un processus ARMA dont le
polynôme
, et de modéliser la
série résultante par un processus ARMA dont le
polynôme ![]() associé ne
possède pas de racine proche de l'unité, et pour
lequel l'approximation des autres coefficients sera plus fine.
associé ne
possède pas de racine proche de l'unité, et pour
lequel l'approximation des autres coefficients sera plus fine.