Section : Modèles ARIMA
Précédent : Définition :
Suivant : Suppression d'un comportement
a-périodique
Si
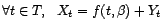 est une série
temporelle qui peut se mettre sous la forme
est une série
temporelle qui peut se mettre sous la forme
avec 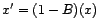 une réalisation d'un
processus stationnaire centré, alors la série
une réalisation d'un
processus stationnaire centré, alors la série
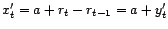 s'écrit
avec
s'écrit
avec 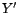 une réalisation d'un processus
stationnaire centré. Partant de ce constat simple, on
poursuit l'étude en modélisant
une réalisation d'un processus
stationnaire centré. Partant de ce constat simple, on
poursuit l'étude en modélisant 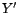 par un processus
par un processus 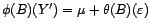 ARMA(
ARMA(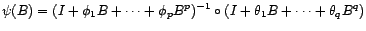 ) décentré, vérifiant
) décentré, vérifiant
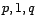 , et on en
déduit le modèle ARIMA(
, et on en
déduit le modèle ARIMA(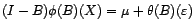 )
décentré
)
décentré
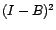 .
.
Si l'on dérive deux fois, autrement dit si l'on fait
passer la série par le filtre 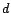 , on
pourra éliminer une tendance binômiale. Plus
généralement, pour supprimer une tendance
polynômiale de degré
, on
pourra éliminer une tendance binômiale. Plus
généralement, pour supprimer une tendance
polynômiale de degré 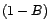 , il suffit
de dériver
, il suffit
de dériver 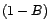 fois.
fois.
Thierry Cabanal-Duvillard
![]() est une série
temporelle qui peut se mettre sous la forme
est une série
temporelle qui peut se mettre sous la forme
![]() , on
pourra éliminer une tendance binômiale. Plus
généralement, pour supprimer une tendance
polynômiale de degré
, on
pourra éliminer une tendance binômiale. Plus
généralement, pour supprimer une tendance
polynômiale de degré ![]() , il suffit
de dériver
, il suffit
de dériver ![]() fois.
fois.