Section : Estimateurs des moindres carrés
Précédent : Exercice 5.
Suivant : Comparaison des deux méthodes,
Soit
 un processus
AR(
un processus
AR(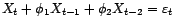 ), vérifiant
), vérifiant
 avec
avec
 bruit blanc. On note
bruit blanc. On note
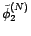 et
et
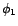 les estimateurs du
maximum de vraisemblance de
les estimateurs du
maximum de vraisemblance de 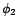 et
et 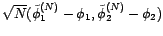 connaissant
connaissant
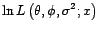 . Quand
. Quand 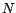 tend vers l'infini,
tend vers l'infini,
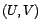 tend en loi vers un vecteur gaussien centré
tend en loi vers un vecteur gaussien centré 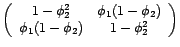 de matrice de covariance
En déduire des domaines de confiance au niveau
de matrice de covariance
En déduire des domaines de confiance au niveau 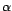 pour
pour 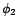 ,
, 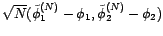 , puis pour le couple
, puis pour le couple
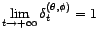 .
.
Thierry Cabanal-Duvillard