Section : Estimateurs des moindres carrés
Précédent : Exercice 4.
Suivant : Exercice 6.
Soit
 un processus
AR(
un processus
AR( ), vérifiant
), vérifiant
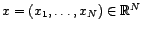 avec
avec
 bruit blanc de variance
bruit blanc de variance
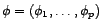 . On pose
. On pose
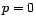 . Soit
. Soit
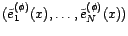 une
réalisation de
une
réalisation de
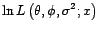 ,
,
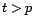 la réalisation correspondante de
la réalisation correspondante de
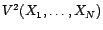 . On note
. On note
![$ {\delta}_i={\mathbb{E}}[\tilde{\varepsilon}_{i}^2]/{\sigma}^2_{\varepsilon}$](img1225.gif) .
.
a) Montrer que pour tout 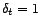 ,
,
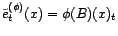 et
et
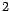 .
.
b) En déduire une expression simple de la
vraisemblance de 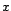 dans ce modèle AR(
dans ce modèle AR( ).
).
Thierry Cabanal-Duvillard
![]() ,
,
![]() et
et
![]() .
.![]() dans ce modèle AR(
dans ce modèle AR(![]() ).
).