1) Déterminer la matrice de covariance du vecteur
aléatoire ![]() , en fonction de
, en fonction de ![]() et
et
![]() . En
déduire la densité de la loi de
. En
déduire la densité de la loi de ![]() .
.
On rappelle que si
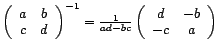 , alors
, alors
![]() .
.
2) On suppose connues deux observations ![]() et
et ![]() du processus
du processus ![]() aux instants 1 et 2. Déterminer les estimateurs du maximum
de vraisemblance de
aux instants 1 et 2. Déterminer les estimateurs du maximum
de vraisemblance de ![]() et
et
![]() en fonction de
en fonction de ![]() et
et ![]() .
.