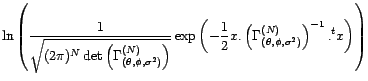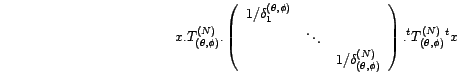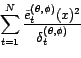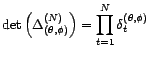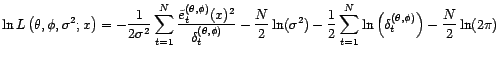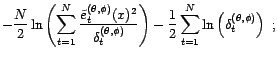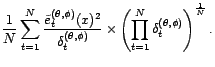Section : Estimateurs des moindres carrés
Précédent : Méthode des moindres carrés
Suivant : Exercice 4.
Si on suppose de plus que  est gaussien, alors
la log-vraisemblance du modèle statistique associé
à
est gaussien, alors
la log-vraisemblance du modèle statistique associé
à
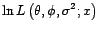 au point
au point
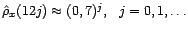 est égale
à
est égale
à
Or
La log-vraisemblance est donc égale à
On choisit comme valeurs de 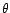 ,
, 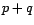 et
et
 celles qui maximisent la fonction
Il ressort facilement des équations de vraisemblance qu'en
ce maximum on a
et que l'on détermine
celles qui maximisent la fonction
Il ressort facilement des équations de vraisemblance qu'en
ce maximum on a
et que l'on détermine 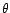 et
et 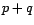 en maximisant
autrement dit, en minimisant
en maximisant
autrement dit, en minimisant
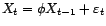
|
(35) |
Section : Estimateurs des moindres carrés
Précédent : Méthode des moindres carrés
Suivant : Exercice 4.
Thierry Cabanal-Duvillard
![]() est gaussien, alors
la log-vraisemblance du modèle statistique associé
à
est gaussien, alors
la log-vraisemblance du modèle statistique associé
à
![]() au point
au point
![]() est égale
à
est égale
à