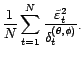 est justement un bruit blanc de variance
est justement un bruit blanc de variance
Soit donc
![]() une série
temporelle qu'on suppose modélisable par
une série
temporelle qu'on suppose modélisable par ![]() un processus ARMA(
un processus ARMA(![]() ) dont on cherche les
autres coefficients. La méthode des moindres carrés
consiste à choisir les valeurs de
) dont on cherche les
autres coefficients. La méthode des moindres carrés
consiste à choisir les valeurs de ![]() et
et ![]() qui minimisent la variance
qui minimisent la variance
![]() du bruit blanc d'innovation. Or
du bruit blanc d'innovation. Or
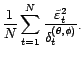 est justement un bruit blanc de variance
est justement un bruit blanc de variance
![]() . L'estimateur le plus naturel de
. L'estimateur le plus naturel de
![]() est donc
est donc
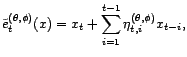
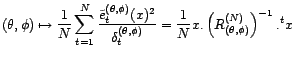
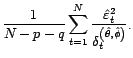 . L'estimateur de
. L'estimateur de
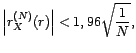 , pour corriger l'écart qui
existe entre
, pour corriger l'écart qui
existe entre