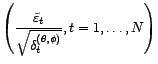Section : Estimateurs des moindres carrés
Précédent : Estimateurs des moindres carrés
Suivant : Méthode des moindres carrés
Soit
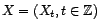 un processus
ARMA(
un processus
ARMA(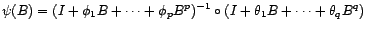 ) tel que
) tel que
avec
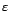 bruit blanc gaussien de
variance
bruit blanc gaussien de
variance
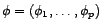 . Notons
. Notons
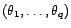 et
et
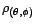 . La fonction
d'autocorrélation de
. La fonction
d'autocorrélation de 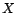 est une fonction de
est une fonction de
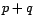 et
et 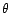 , qu'on
notera
, qu'on
notera
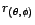 . De même,
la fonction d'autocorrélation partielle de
. De même,
la fonction d'autocorrélation partielle de 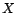 ,
qui se calcule à partir de la fonction
d'autocorrélation, est-elle une fonction de
,
qui se calcule à partir de la fonction
d'autocorrélation, est-elle une fonction de 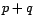 et
et 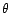 , qu'on notera
, qu'on notera
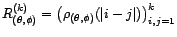 . La matrice de
corrélation d'ordre
. La matrice de
corrélation d'ordre 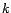 sera notée
sera notée
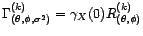 , et la matrice de covariance par
, et la matrice de covariance par
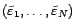 .
.
Soit
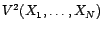 la base
orthogonale de
la base
orthogonale de
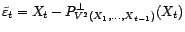 construite par
l'algorithme des innovations :
construite par
l'algorithme des innovations :
Il existe des coefficients
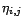 et
et
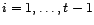 tels que pour tout
tels que pour tout
 et
et
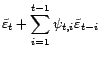 , on ait
, on ait
Là encore, ces coefficients ne dépendent que de 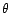 et
et 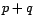 et on les notera
plutôt
et on les notera
plutôt
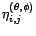 et
et
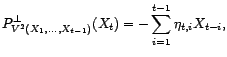 . En effet,
ce qui implique que les coefficients
. En effet,
ce qui implique que les coefficients
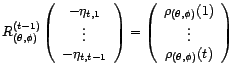 sont déterminés
par les équations de Yule-Walker
Les coefficients
sont déterminés
par les équations de Yule-Walker
Les coefficients
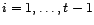 sont donc bien fonction de
sont donc bien fonction de
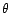 et
et 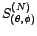 uniquement. Quant aux coefficients
uniquement. Quant aux coefficients
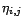 , ils peuvent être
calculés à partir des
, ils peuvent être
calculés à partir des
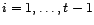 . En effet, notons
. En effet, notons
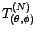 et
et
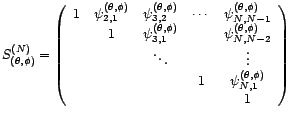 les matrices
triangulaires supérieures
et
Il s'agit bien sûr des matrices de passage entre les deux
bases
les matrices
triangulaires supérieures
et
Il s'agit bien sûr des matrices de passage entre les deux
bases
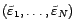 et
et
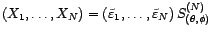 :
et inversement
En particulier,
:
et inversement
En particulier,
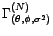 . Les coefficients
. Les coefficients
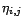 sont donc bien fonction des
sont donc bien fonction des
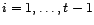 et donc de
et donc de 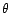 et
et 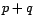 . On en déduit
aussi que
. On en déduit
aussi que
avec
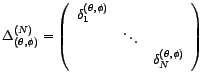 la
matrice diagonale
la
matrice diagonale
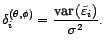
avec
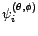
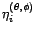 et
et
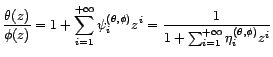 les
coefficients apparaissant dans les représentations MA(
les
coefficients apparaissant dans les représentations MA(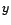 ) et AR(
) et AR(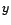 ) de
) de 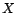 :
:
Section : Estimateurs des moindres carrés
Précédent : Estimateurs des moindres carrés
Suivant : Méthode des moindres carrés
Thierry Cabanal-Duvillard
![]() un processus
ARMA(
un processus
ARMA(![]() ) tel que
) tel que
![]() la base
orthogonale de
la base
orthogonale de
![]() construite par
l'algorithme des innovations :
construite par
l'algorithme des innovations :
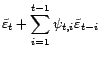 , on ait
, on ait 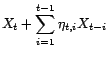
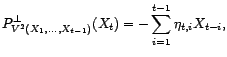 . En effet,
. En effet,
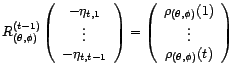 sont déterminés
par les équations de Yule-Walker
sont déterminés
par les équations de Yule-Walker
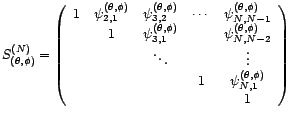 les matrices
triangulaires supérieures
les matrices
triangulaires supérieures
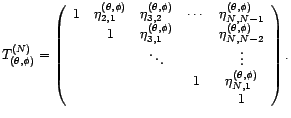
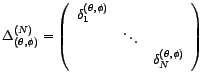 la
matrice diagonale
la
matrice diagonale
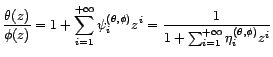 les
coefficients apparaissant dans les représentations MA(
les
coefficients apparaissant dans les représentations MA(