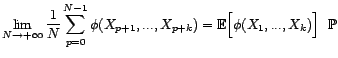 mesurable bornée
mesurable bornée |
|||
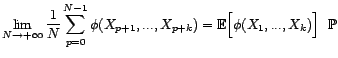 mesurable bornée
mesurable bornée |
|||
Pour qu'un processus stationnaire ![]() soit
ergodique, il suffit essentiellement que
soit
ergodique, il suffit essentiellement que ![]() et
et
![]() soient asymptotiquement
indépendants quand
soient asymptotiquement
indépendants quand
![]() tend vers l'infini. C'est
évidemment le cas si
tend vers l'infini. C'est
évidemment le cas si ![]() est une famille de
variables aléatoires i.i.d. Un contre-exemple simple est
donné par le processus
est une famille de
variables aléatoires i.i.d. Un contre-exemple simple est
donné par le processus
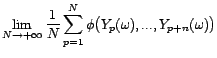 :
il est stationnaire, mais
:
il est stationnaire, mais
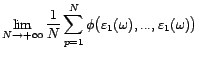
|
|||