Section : Filtres
ARMA
Précédent : Démonstration du théorème
Suivant : Définition :
Un filtre autorégressif 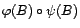 d'ordre
d'ordre  est l'inverse d'un filtre MA(
est l'inverse d'un filtre MA( ) :
avec
) :
avec
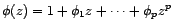 , et
, et
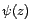 ne
s'annulant pas sur le cercle unité. On le dit AR(
ne
s'annulant pas sur le cercle unité. On le dit AR( ). Il est causal si
). Il est causal si 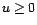 ne
s'annule pas sur le disque unité. Sa transformée en
ne
s'annule pas sur le disque unité. Sa transformée en
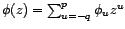 est l'inverse d'un polynôme :
est l'inverse d'un polynôme :
car
 .
.
Si un filtre AR( ) est causal, il
s'écrit comme
) est causal, il
s'écrit comme
On parle alors de représentation sous forme MA(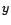 ).
).
Autrement dit, si 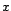 et
et 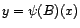 sont
deux éléments de
sont
deux éléments de
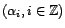 , on a les
équivalences
, on a les
équivalences
Section : Filtres
ARMA
Précédent : Démonstration du théorème
Suivant : Définition :
Thierry Cabanal-Duvillard
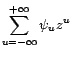
 .
.
![]() ) est causal, il
s'écrit comme
) est causal, il
s'écrit comme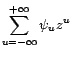
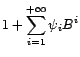
![]() et
et ![]() sont
deux éléments de
sont
deux éléments de
![]() , on a les
équivalences
, on a les
équivalences