Section : Filtres
ARMA
Précédent : Définition :
Suivant : Représentation causale et inversible
Un filtre 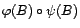 est dit de type ARMA(
est dit de type ARMA(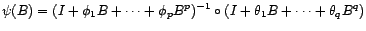 ) s'il est le produit de composition d'un filtre
AR(
) s'il est le produit de composition d'un filtre
AR( ) avec un filtre MA(
) avec un filtre MA(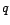 ) :
Sa transformée en
) :
Sa transformée en 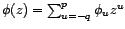 est le rapport des
deux polynômes :
avec
est le rapport des
deux polynômes :
avec
On pourra toujours supposer que les deux polynômes
 et
et 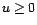 n'ont pas de racine commune (dans le cas contraire, après
simplification,
n'ont pas de racine commune (dans le cas contraire, après
simplification, 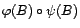 apparaît comme un
filtre ARMA d'ordres inférieurs).
apparaît comme un
filtre ARMA d'ordres inférieurs).
Si le filtre AR( )
)
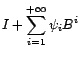 est causal, il en est de
même de
est causal, il en est de
même de 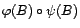 , et il en existe une
représentation MA(
, et il en existe une
représentation MA(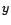 ) :
) :
De façon symétrique, si
 ne s'annule pas sur le disque
unité, alors
ne s'annule pas sur le disque
unité, alors
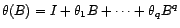 est un filtre inversible, et son
inverse est causal. Le filtre
est un filtre inversible, et son
inverse est causal. Le filtre
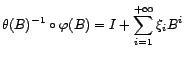 est alors
causal, et peut s'écrire
On parle de représentation AR(
est alors
causal, et peut s'écrire
On parle de représentation AR(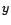 ).
).
Soient 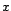 et
et 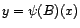 deux
éléments de
deux
éléments de
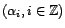 , alors
, alors
Section : Filtres
ARMA
Précédent : Définition :
Suivant : Représentation causale et inversible
Thierry Cabanal-Duvillard
![]() )
)
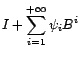 est causal, il en est de
même de
est causal, il en est de
même de ![]() , et il en existe une
représentation MA(
, et il en existe une
représentation MA(![]() ) :
) :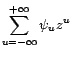
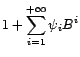
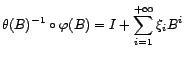 est alors
causal, et peut s'écrire
est alors
causal, et peut s'écrire
![]() et
et ![]() deux
éléments de
deux
éléments de
![]() , alors
, alors