Section : Filtres
ARMA
Précédent : Définition :
Suivant : Démonstration du théorème
- Si
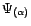 , alors
, alors
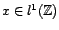 n'est pas surjective. En
effet, s'il existait
n'est pas surjective. En
effet, s'il existait
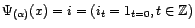 tel que
tel que
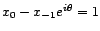 ,
alors
,
alors
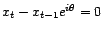 et
et
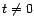 quel que soit
quel que soit
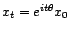 ; il en résulte
; il en résulte
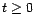 si
si 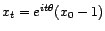 et
et
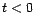 si
si 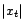 . Ce qui est en contradiction avec le fait que
. Ce qui est en contradiction avec le fait que
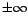 tend vers 0 quand
tend vers 0 quand 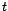 tend vers
tend vers 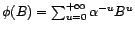 , puisque
, puisque 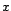 appartient à
appartient à
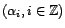 .
.
- Si
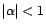 , alors on
définit le filtre linéaire
, alors on
définit le filtre linéaire
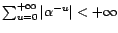 (on
vérifie bien que
(on
vérifie bien que
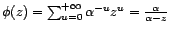 . Ce
filtre est de transformée en
. Ce
filtre est de transformée en 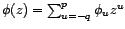 égale
à
égale
à
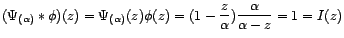 . On en découle que
Autrement dit,
. On en découle que
Autrement dit,
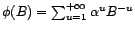 . Le filtre
. Le filtre 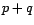 est donc l'inverse de
est donc l'inverse de
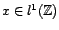 et il est causal.
et il est causal.
- Si
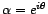 , alors on raisonne
de même avec le filtre
, alors on raisonne
de même avec le filtre
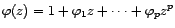 .
.
Corollaire 2.III.5
Un filtre MA(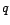 ) est inversible si et seulement si
sa transformée en
) est inversible si et seulement si
sa transformée en 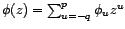 n'a pas de racine
de module
n'a pas de racine
de module 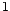 . Son inverse est causal si et
seulement si toutes ses racines sont de module strictement
supérieur à
. Son inverse est causal si et
seulement si toutes ses racines sont de module strictement
supérieur à 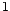 .
.
Thierry Cabanal-Duvillard