Section : Filtres
ARMA
Précédent : Filtres ARMA
Suivant : Démonstration
On appelle filtre MA(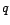 ) tout filtre
) tout filtre
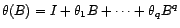 de la forme
avec
de la forme
avec
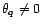 . Sa transformée en
. Sa transformée en
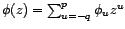 est un polynôme :
est un polynôme :
Soit 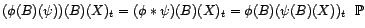 un filtre MA(
un filtre MA(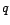 ), et soient
), et soient
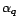 ,...,
,...,
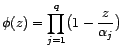 les racines
(éventuellement complexes) de sa transformée en
les racines
(éventuellement complexes) de sa transformée en 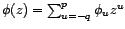 :
:
Cela signifie que 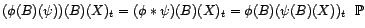 se décompose
en filtres MA(
se décompose
en filtres MA(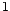 ) de la façon suivante
- on a ici étendu la définition des filtres puisqu'on
les considère à coefficients dans
) de la façon suivante
- on a ici étendu la définition des filtres puisqu'on
les considère à coefficients dans
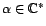 . Le filtre
. Le filtre 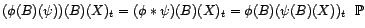 est inversible si et seulement si tous les filtres
de cette décomposition le sont.
est inversible si et seulement si tous les filtres
de cette décomposition le sont.
Théorème 2.III.4 Soit
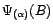 , et notons
, et notons
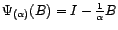 le filtre MA(
le filtre MA(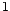 ) défini par
) défini par
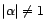
-
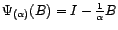 est inversible si et
seulement si
est inversible si et
seulement si
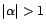 .
.
- Le filtre inverse est causal si et seulement si
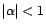 et purement non
réalisable si et seulement si
et purement non
réalisable si et seulement si
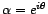 .
.
Thierry Cabanal-Duvillard
![]() un filtre MA(
un filtre MA(![]() ), et soient
), et soient
![]() ,...,
,...,
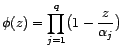 les racines
(éventuellement complexes) de sa transformée en
les racines
(éventuellement complexes) de sa transformée en ![]() :
: