Section : Filtres
et stationnarité
Précédent : Remarque :
Suivant : Filtres ARMA
D'après la démonstration du théorème
![[*]](file:/usr/share/latex2html/icons/crossref.gif) , on a
, on a
Comme on a
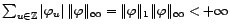 et
et
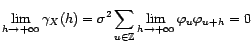 , on peut appliquer le théorème de convergence
dominée, et en déduire
car
, on peut appliquer le théorème de convergence
dominée, et en déduire
car
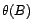 . Il s'ensuit que
. Il s'ensuit que
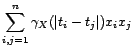 converge aussi vers 0 quand
converge aussi vers 0 quand 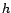 tend vers l'infini.
tend vers l'infini.
Thierry Cabanal-Duvillard
![]() , on a
, on a converge aussi vers 0 quand
converge aussi vers 0 quand