Section : Filtres
et stationnarité
Précédent : Filtres et stationnarité
Suivant : Rappels
: Théorème de
Soit
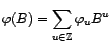 l'ensemble
des suites absolument convergentes. On appelle filtre
linéaire tout opérateur de la forme
où
l'ensemble
des suites absolument convergentes. On appelle filtre
linéaire tout opérateur de la forme
où
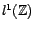 .
.
Comme exemple, il y a bien évidemment les moyennes
mobiles finies.
Théorème
2.III.1
- Tout filtre linéaire est un endomorphisme de
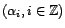 .
.
- L'image par un filtre linéaire d'un processus faiblement
stationnaire est un processus faiblement stationnaire.
Thierry Cabanal-Duvillard