Section : Filtres
et stationnarité
Précédent : Définition :
Suivant : Démonstration du théorème
Si
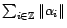 est une
famille dénombrable de réels positifs, alors la
nature et la valeur de leur série ne dépend pas de
l'ordre de leur sommation. S'il s'agit d'une famille
d'éléments d'un espace vectoriel normé complet
(i.e. un espace de Banach), et si la série
est une
famille dénombrable de réels positifs, alors la
nature et la valeur de leur série ne dépend pas de
l'ordre de leur sommation. S'il s'agit d'une famille
d'éléments d'un espace vectoriel normé complet
(i.e. un espace de Banach), et si la série
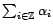 est convergente, alors la valeur de la série
est convergente, alors la valeur de la série
 ne
dépend pas de l'ordre de sommation, et elle est
convergente.
ne
dépend pas de l'ordre de sommation, et elle est
convergente.
Thierry Cabanal-Duvillard