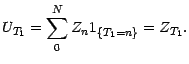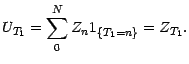Section : Un
deuxième temps d'arrêt
Précédent : Un deuxième temps d'arrêt
Suivant : Mathématiques des marchés
financiers
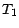 est optimal ; il n'existe pas d'autre
temps d'arrêt optimal
est optimal ; il n'existe pas d'autre
temps d'arrêt optimal 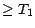 .
.
Démonstration :Nous allons utiliser la
caractérisation 2.5.2.2 des temps d'arrêt
optimaux .
-
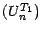 est une martingale : par
définition de
est une martingale : par
définition de 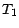 , on a les implications
Il en résulte que
, on a les implications
Il en résulte que
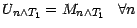 , ce qui
s'écrit encore
, ce qui
s'écrit encore
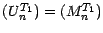 , d'où le
résultat .
, d'où le
résultat .
-
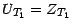 : On a
: On a
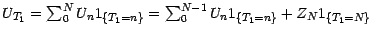 . Plaçons nous , pour
. Plaçons nous , pour 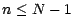 , sur
l'événement
, sur
l'événement 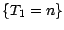 , sur
lequel
, sur
lequel 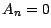 (et donc
(et donc 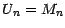 ) ,
) ,
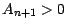 et où l'on peut donc
écrire
Mais comme
et où l'on peut donc
écrire
Mais comme
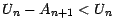 , on a
nécessairement
, on a
nécessairement 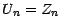 ; il en
résulte que
; il en
résulte que
- Il nous reste à montrer le caractère maximal de
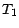 : Si
: Si 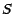 un temps
d'arrêt tel que
un temps
d'arrêt tel que
![$ S\geq T_1\;et\;\textbf{P}[S>T_1]>0$](img779.gif) ,
on aura
,
on aura
![$ \textbf{E}[U_S]=\textbf{E}[M_S-A_S]<\textbf{E}[M_S]=\textbf{E}[M_0]=\textbf{E}[U_0]$](img780.gif) , si bien que
, si bien que 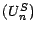 ne peut pas être une
martingale ;
ne peut pas être une
martingale ; 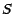 n'est donc pas optimal , C.Q.F.D.
n'est donc pas optimal , C.Q.F.D.
Jacques Azéma