Section : Variables
aléatoires -mesurables
Précédent : Variables aléatoires -mesurables
Suivant : Conditionnement par une algèbre
Nous allons montrer que ce sont tout simplement les v.a. que nous
avons appelées jusqu'ici de manière peu
élégante "fonctions déterministes de 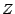 " .
" .
Proposition : Soit 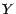 une v.a.r. ;
les deux propriétés suivantes sont
équivalentes
une v.a.r. ;
les deux propriétés suivantes sont
équivalentes
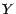 est
est
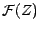 -mesurable .
-mesurable .- Il existe une fonrtion numérique
 sur
sur
 telle que
telle que
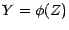 .
.
Démonstration : Si 2. est
vérifiée, 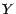 est constante sur les atomes
de
est constante sur les atomes
de
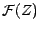 , d'où 1. ;
réciproquement, posons
, d'où 1. ;
réciproquement, posons
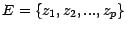 ; si
; si 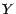 est
est
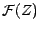 - mesurable, il existe, par
définition,
- mesurable, il existe, par
définition, 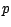 constantes
constantes
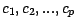 telles que
telles que
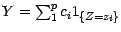 ; il en
résulte que
; il en
résulte que 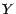 vérifie 2., avec
vérifie 2., avec
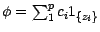 , (Cf.(
, (Cf.(![[*]](file:/usr/share/latex2html/icons/crossref.gif) ))
))
Jacques Azéma
une v.a.r. ; les deux propriétés suivantes sont équivalentes
est constante sur les atomes de
, d'où 1. ; réciproquement, posons
; si
est
- mesurable, il existe, par définition,
constantes
telles que
; il en résulte que
vérifie 2., avec
, (Cf.(
))