Section : Conditionnement par une variable
Précédent : Démonstrations
Suivant : Algèbres et partitions
Supposons
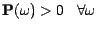 et posons
et posons
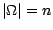 ; On notera
; On notera 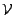 l'espace vectoriel des v.a.r sur
l'espace vectoriel des v.a.r sur  et
et 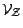 le sous ensemble de
le sous ensemble de 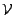 formé des fonctions déterministes de
formé des fonctions déterministes de
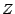 ; on posera enfin
; on posera enfin
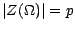 .
.
- On munit
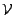 du produit scalaire défini
par
du produit scalaire défini
par
![$ <X , Y>=\textbf{E}[XY]$](img362.gif) ; donner la
dimension de l'espace euclidien ainsi défini ainsi que celle
du sous espace
; donner la
dimension de l'espace euclidien ainsi défini ainsi que celle
du sous espace 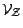 .
.
- Soit
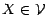 ; montrer que
; montrer que
![$ \textbf {E}[X\vert Z]$](img321.gif) est la projection
eucidienne de
est la projection
eucidienne de  sur
sur
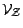 .
.
- On note
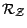 le sous espace de
le sous espace de 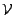 formé des v.a.r. qui sont des fonctions affines
de
formé des v.a.r. qui sont des fonctions affines
de 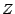 . Quelle est sa dimension ? Montrer qur la
projection eucidienne
. Quelle est sa dimension ? Montrer qur la
projection eucidienne ![$ R[X\vert Z]$](img366.gif) de
de  sur
sur 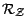 est donnée par
l'égalité
quand on a posé
est donnée par
l'égalité
quand on a posé
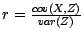
- Montrer sans calculs l'inégalité
![$ \textbf{E}[(X-\textbf{E}[X\vert Z])^2]\leq \textbf{E}[(X-R[X\vert Z])^2]$](img370.gif) .
.
- Montrer que
![$ \textbf{E}[X\vert Z]=R[X\vert Z]$](img371.gif) si
si
Jacques Azéma