Section : Conditionnement par une variable
Précédent : Proposition
Suivant : Démonstrations

Proposition :

1. $\textbf{E}[aX+bX'\vert Z]=a\textbf{E}[X\vert Z]+b\textbf{E}[X'\vert Z]\;\;\forall a\in{\mathbb{R}}\;\; \forall b\in {\mathbb{R}}$
2. $X\geq 0 \Longrightarrow \textbf{E}[X\vert Z]\geq 0$
3. $\textbf{E}[\textbf{E}[X\vert Z]]=\textbf{E}[X]$
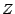4. Si $X$ et $Z$ sont indépendantes , $\textbf {E}[X\vert Z]$=E[X]
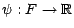5. Soit $\psi :F\to {\mathbb{R}}$ une fonction numérique sur 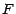$F$ ; on a

   $$\textbf{E}[X\psi(Z)\vert Z]=\psi(Z)\textbf{E}[X\vert Z] .$$ (2.13)

   
   En particulier
   $$\textbf{E}[\psi(Z)\vert Z]=\psi(Z).$$
6. () peut être généralisée comme suit ; on associe à la fonction $H:\Omega \times F\to {\mathbb{R}}$
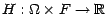
   la variable aléatoire réelle 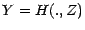$Y=H(.,Z)$ ; si l'on pose alors $K(.,i)= \textbf{E}[H(.,i)\vert Z]$ , on a

   $$\textbf{E}[Y\vert Z]=K(.,Z)$$ (2.14)

   
   
7. Soient X une v.a à valeurs dans $E$ indépendante de 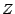$Z$ et $h:E\times F \to {\mathbb{R}}$ ; on pose
   $v(i)=\textbf{E}[h(X,i)] \;\;\;(i\in F)$ . On a alors

   $$\textbf{E}[h(X,Z)\vert Z]=v(Z)$$ (2.15)