Section : Une
caractérisation de
Précédent : Une caractérisation de
Suivant : Proposition :
![$ \textbf {E}[X\vert Z]$](img321.gif) est l'unique v.a.r
est l'unique v.a.r
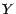 vérifiant les 2
propriétés suivantes :
vérifiant les 2
propriétés suivantes :
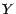 est une fonction déterministe de
est une fonction déterministe de
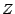
-
![$ \textbf {E}[Y\psi (Z)]=\textbf {E}[X\psi (Z)]\;\;\;\;\forall \psi\; : E\to {\mathbb{R}}$](img322.gif)
Démonstration : Il est clair d'après sa
définition que
![$ Y=\textbf {E}[X\vert Z]$](img323.gif) vérifie la
propriété 1. D'autre part, les égalités
montrent que
vérifie la
propriété 1. D'autre part, les égalités
montrent que 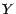 vérifie 2.
Réciproquement, soit
vérifie 2.
Réciproquement, soit 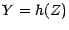 une v.a.r.
vérifiant 1. et 2. ; cette dernière
propriété écrite pour
une v.a.r.
vérifiant 1. et 2. ; cette dernière
propriété écrite pour
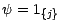 conduit à
l'égalité (Cf. (
conduit à
l'égalité (Cf. (![[*]](file:/usr/share/latex2html/icons/crossref.gif) ))
))
![$ h(j)\textbf {P}[Z=j]=\textbf {E}[X1_{[Z=j]}]$](img327.gif) , si bien que
, si bien que
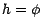 , d'où le résultat.
, d'où le résultat.
Énonçons maintenant quelques
propriétés simples de cette espérance
conditionnelle.
Jacques Azéma