Section : Conditionnement par une variable
Précédent : Conditionnement par une variable
Suivant : Une
caractérisation de
Au paragraphe précédent, nous avons souvent
été amenés à considérer des
expressions de la forme
![$ \textbf{E}[X \vert Z=i]$](img306.gif) où
où  est une v.a. réelle et
est une v.a. réelle et 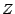 une
v.a. quelconque à valeurs dans un ensemble fini
une
v.a. quelconque à valeurs dans un ensemble fini 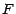 . En général le résultat dépend
de
. En général le résultat dépend
de 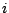 , ce qui nous amène à
définir une fonction
, ce qui nous amène à
définir une fonction
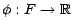 par
par
![$\displaystyle \textbf{E}[X \vert Z=i] =\phi (i)$](img309.gif) |
(2.11) |
(On posera, par convention,
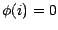 si
si
![$ \textbf{P}[Z=i]=0$](img311.gif) ).
).
Il est alors naturel de poser, de manière plus
ramassée,
![$\displaystyle \textbf{E}[X\vert Z]=\phi (Z)$](img312.gif) |
(2.12) |
Puisque le second membre de (![[*]](file:/usr/share/latex2html/icons/crossref.gif) ) est une v.a.
qui vaut
) est une v.a.
qui vaut 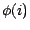 , (c'està dire
, (c'està dire
![$ \textbf{E}[X \vert Z=i]$](img306.gif) ) "quand
) "quand 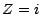 " . Revenons un instant aux exemples du paragraphe
2.1 pour s'habituer à cette notation . Les
égalités (
" . Revenons un instant aux exemples du paragraphe
2.1 pour s'habituer à cette notation . Les
égalités (![[*]](file:/usr/share/latex2html/icons/crossref.gif) ) , (
) , (![[*]](file:/usr/share/latex2html/icons/crossref.gif) ) , (
) , (![[*]](file:/usr/share/latex2html/icons/crossref.gif) ) , (
) , (![[*]](file:/usr/share/latex2html/icons/crossref.gif) ) deviennent
ainsi respectivement
On aura noté que la v.a. conditionnante
) deviennent
ainsi respectivement
On aura noté que la v.a. conditionnante 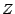 peut prendre ses valeurs dans un espace produit ; c'est le cas dans
la formule (
peut prendre ses valeurs dans un espace produit ; c'est le cas dans
la formule (![[*]](file:/usr/share/latex2html/icons/crossref.gif) )
où l'on posera
)
où l'on posera
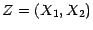 , ce qui conduit à
l'égalité
, ce qui conduit à
l'égalité
Section : Conditionnement par une variable
Précédent : Conditionnement par une variable
Suivant : Une
caractérisation de
Jacques Azéma
![\begin{displaymath}\textbf{P}[S_p=k \vert S_n]=\frac{ \left( \begin{array}{c} p\... ...ay}\right)}{\left( \begin{array}{c} n\\ S_n \end{array}\right)}\end{displaymath}](img315.gif)