Section : Indépendance
Précédent : Exemple: une autre approche
Suivant : Variance
d'une somme de
Soient  et
et 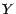 sont 2 variables
aléatoires indépendantes à valeurs dans
sont 2 variables
aléatoires indépendantes à valeurs dans  ,
, 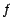 et
et 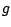 deux fonctions
numériques sur
deux fonctions
numériques sur  alors
alors
En particulier , si  et
et 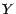 sont
réelles ,
sont
réelles ,
![$ \textbf{E}[XY]=\textbf{E}[X]\textbf{E}[Y]$](img238.gif) .
.
Après avoir remarqué qu'il suffit de montrer la
deuxième assertion , posons 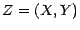 ; on a
On notera que si l'une des 2 v.a. est centrée ,
; on a
On notera que si l'une des 2 v.a. est centrée ,
![$ \textbf{E}[XY]=0$](img241.gif)
Jacques Azéma
![]() et
et ![]() sont 2 variables
aléatoires indépendantes à valeurs dans
sont 2 variables
aléatoires indépendantes à valeurs dans ![]() ,
, ![]() et
et ![]() deux fonctions
numériques sur
deux fonctions
numériques sur ![]() alors
alors
![$\displaystyle \textbf{E}[XY]=\sum_{x,y}xy\Pi_Z(x,y)=\sum_{x,y}xy\Pi_X(x)\Pi_Y(y)=(\sum_x x\Pi_x(x))(\sum_y y\Pi_Y)(y)= \textbf{E}[X]\textbf{E}[Y]$](img240.gif)