Section : Indépendance
Précédent : Espérance d'un produit de
Suivant : Exercice:
Soit
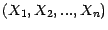 une famille de
une famille de  v.a.r. indépendantes ; on pose
v.a.r. indépendantes ; on pose
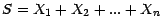 .
.
On a alors
On se ramène en effet aisément au cas où les
v.a. 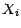 sont centrées ;la fin du calcul
va ensuite de soi , compte tenu du point précédent .
L'hypothèse d'indépendance est ici essentielle .
sont centrées ;la fin du calcul
va ensuite de soi , compte tenu du point précédent .
L'hypothèse d'indépendance est ici essentielle .
Jacques Azéma