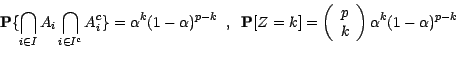Section : Indépendance
Précédent : Proposition
Suivant : Espérance d'un produit de
Soit(
 ) une suite de
) une suite de  événements indépendants de
même probabilité
événements indépendants de
même probabilité  ; on pose
; on pose
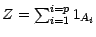 . Nous allons voir
que
. Nous allons voir
que 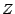 suit une loi binomiale de
paramètres
suit une loi binomiale de
paramètres
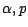 . En vertu de
l'indépendance des
. En vertu de
l'indépendance des 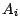 , on a en effet ,
si
, on a en effet ,
si 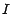 est une partie de
est une partie de
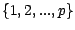 de cardinal
de cardinal 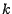 ,
,
Le fait que 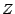 admette même loi que la v.a.
admette même loi que la v.a.
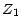 du sondage (exemple b)), n'est
pas dû au hasard. Dans ce modèle, en effet, P
est la loi uniforme sur
du sondage (exemple b)), n'est
pas dû au hasard. Dans ce modèle, en effet, P
est la loi uniforme sur
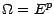 et les variables
aléatoires
et les variables
aléatoires 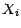 sont les applications
coordonnées ; d'après la proposition
précédente , ces v.a. sont donc indépendantes
et suivent une loi uniforme sur
sont les applications
coordonnées ; d'après la proposition
précédente , ces v.a. sont donc indépendantes
et suivent une loi uniforme sur  . Les
événements
. Les
événements
![$ [X_i\in E_1]$](img234.gif) sont donc indépendants
de probabilité
sont donc indépendants
de probabilité
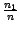 , ce qui permet d'appliquer la
formule ci-dessus à la v.a.
, ce qui permet d'appliquer la
formule ci-dessus à la v.a.
![$ Z_1=\sum_i1_{[X_i\in E_1]}$](img235.gif) .
.
Jacques Azéma
![]() ) une suite de
) une suite de ![]() événements indépendants de
même probabilité
événements indépendants de
même probabilité ![]() ; on pose
; on pose
![]() . Nous allons voir
que
. Nous allons voir
que ![]() suit une loi binomiale de
paramètres
suit une loi binomiale de
paramètres
![]() . En vertu de
l'indépendance des
. En vertu de
l'indépendance des ![]() , on a en effet ,
si
, on a en effet ,
si ![]() est une partie de
est une partie de
![]() de cardinal
de cardinal ![]() ,
,