Section : Valeur
d'une option américaine
Précédent : Valeur d'une option américaine
Suivant : Exercice
- Soit
 une option américaine ;
définissons par récurrence descendante la suite
une option américaine ;
définissons par récurrence descendante la suite 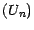 par les égalités
On dira que
par les égalités
On dira que 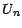 est la valeur de l'option
est la valeur de l'option  à la date
à la date 
-
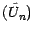 est , sous P* ,
l'enveloppe de Snell de la suite
est , sous P* ,
l'enveloppe de Snell de la suite
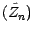
On vérifie en effet facilement que
![$ \tilde U_{n-1}=\tilde Z_{n-1}\vee \textbf{E*}[\tilde U_n\vert {\cal F}_{n-1}]$](img1178.gif) .
.
Sous-sections
Jacques Azéma