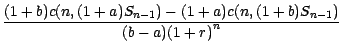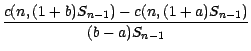Section : Calculs
explicites
Précédent : Théorème :
Suivant : Les
options américaines
Rappelons que l'émetteur de notre call n'a pu le vendre
à un prix raisonnable que parceque nous lui avons dit qu'il
existait , (puisque le marché est complet), une
stratégie de couverture de cette option . Mais si le
mathématicien se satisfait aisément d'un
théorème d'existence , la banque qui l'emploie
exigera qu'il lui fournisse explicitement le moyen de se couvrir ;
c'est ce que nous allons faire maintenant . Soit
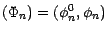 une
statégie prévisible simulant l'option d'achat ; on a
ce que l'on écrira
une
statégie prévisible simulant l'option d'achat ; on a
ce que l'on écrira
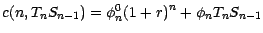 ;
rappelons nous que
;
rappelons nous que 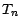 ne prend que les 2
valeurs
ne prend que les 2
valeurs 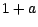 et
et 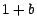 ; on a donc
Plaçons nous sous
; on a donc
Plaçons nous sous
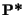 et prenons les espérances
conditionnelles des 2 égalités
précédentes par rapport à l'algèbre
et prenons les espérances
conditionnelles des 2 égalités
précédentes par rapport à l'algèbre
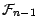 ; compte tenu de ce que
; compte tenu de ce que
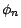 est
est
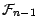 -mesurable
-mesurable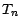 est indépendante de
est indépendante de
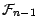
on obtient
Il reste à résoudre ce système linéaire
à 2 inconnues pour obtenir
On notera que l'on obtient bien 2 suites prévisibles ; il y
a plus : à l'instant  , il suffit de
connaitre les cours de l'instant immédiatement
précédent pour réorganiser son portefeuille .
Nous laissons en exercice la couverture d'une option de vente .
, il suffit de
connaitre les cours de l'instant immédiatement
précédent pour réorganiser son portefeuille .
Nous laissons en exercice la couverture d'une option de vente .
Section : Calculs
explicites
Précédent : Théorème :
Suivant : Les
options américaines
Jacques Azéma
![$\displaystyle \lbrace \begin{array}{l} c(n,(1+a)S_{n-1})1_{[T_n=1+a]}=[\phi^0_n... ...1_{[T_n=1+b]}=[\phi^0_n{(1+r)}^n+(1+b)\phi_n S_{n-1}]1_{[T_n=1+b]} \end{array}$](img1161.gif)
 \end{array}\end{displaymath}](img1162.gif)