Section : Calculs
explicites
Précédent : Lemme
Suivant : Couverture du call
Le prix d'un call européen est donné par la formule
![$\displaystyle C_n=\frac{1}{{(1+r)}^{N-n}}\sum_{j=0}^{j=N-n} \left( \begin{array... ...\\ j\\ \end{array} \right)p^j{(1-p)}^{N-n-j}{[S_n{(1+a)}^j{(1+b)}^{N-n-j}-K]}^+$](img1151.gif)
|
(5.1) |
Démonstration :
Posons alors
de sorte que ,(cf (13)) ,
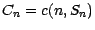 . Le lemme
précédent appliqué à la fonction
symétrique
. Le lemme
précédent appliqué à la fonction
symétrique
conduit à l'égalité
On en déduit immédiatement la formule 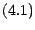 . Il est inutile de recommencer un calcul analogue pour
obtenir le prix du put : il est plus simple de se servir de la
formule de parité .
. Il est inutile de recommencer un calcul analogue pour
obtenir le prix du put : il est plus simple de se servir de la
formule de parité .
Jacques Azéma
![$\displaystyle C_n=\frac{1}{{(1+r)}^{N-n}}\sum_{j=0}^{j=N-n} \left( \begin{array... ...\\ j\\ \end{array} \right)p^j{(1-p)}^{N-n-j}{[S_n{(1+a)}^j{(1+b)}^{N-n-j}-K]}^+$](img1151.gif)
![$\displaystyle C_n=\frac{1}{{(1+r)}^{N-n}}\sum_{j=0}^{j=N-n} \left( \begin{array... ...\\ j\\ \end{array} \right)p^j{(1-p)}^{N-n-j}{[S_n{(1+a)}^j{(1+b)}^{N-n-j}-K]}^+$](img1151.gif)
. Le lemme précédent appliqué à la fonction symétrique
![\begin{displaymath}c(n,s)=\frac{1}{{(1+r)}^{N-n}}\sum_{j=0}^{j=N-n} \left( \begi... ...}\right ) p^j{(1-p)}^{N-n-j}{[s{(1+a)}^j{(1+b)}^{N-n-j}-K]}^+ .\end{displaymath}](img1156.gif)