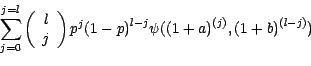Section : Calculs
explicites
Précédent : Calculs explicites
Suivant : Théorème :
Soit
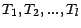 une suite de
une suite de 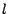 variables aléatoires indépendantes
équidistribuées de loi commune
variables aléatoires indépendantes
équidistribuées de loi commune 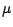 , et soit
, et soit 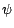 une fonction
numérique symétrique sur
une fonction
numérique symétrique sur
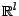 ;on a , si l'on note
;on a , si l'on note 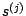 l'élément
l'élément
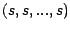 de
de
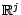
Démonstration : Posons
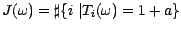 ; la
démonstration est très simple si l'on veut bien
réfléchir aux 2 points suivants :
; la
démonstration est très simple si l'on veut bien
réfléchir aux 2 points suivants :
- la loi de
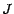 est binomiale ; on peut en effet
écrire
est binomiale ; on peut en effet
écrire
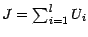 quand on a posé
quand on a posé
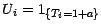 . Il reste alors
à remarquer que
. Il reste alors
à remarquer que
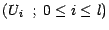 constitue une
suite indépendante de v.a. de Bernoulli telles que
constitue une
suite indépendante de v.a. de Bernoulli telles que
![$ \textbf{P}[U_i=1]=p\;\;,\;\;\textbf{P}[U_i=0]=1-p$](img1145.gif)
- compte tenu de la symétrie supposée sur
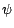 , la v.a
, la v.a
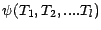 est une fonction de
est une fonction de
 ; plus précisément
; plus précisément
On a donc
Jacques Azéma
![]() une suite de
une suite de ![]() variables aléatoires indépendantes
équidistribuées de loi commune
variables aléatoires indépendantes
équidistribuées de loi commune ![]() , et soit
, et soit ![]() une fonction
numérique symétrique sur
une fonction
numérique symétrique sur
![]() ;on a , si l'on note
;on a , si l'on note ![]() l'élément
l'élément
![]() de
de
![]()
![$\displaystyle \textbf{E}[\psi (T_1 , T_2 , .... , T_l)]= \sum_{j=0}^{j=l} \left... ...} \right) p^j{(1-p)}^{l-j}\psi({(1+a)}^{(j)} , {(1+b)}^{(l-j)})\hspace{1cm}(39)$](img1139.gif)
; la démonstration est très simple si l'on veut bien réfléchir aux 2 points suivants :
![$\displaystyle \sum_{j=0}^{j=l}\psi({(1+a)}^{(j)} , {(1+b)}^{(l-j)}) \textbf{P}[J=j]$](img1149.gif)