Supposons
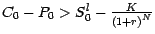 .
.
Soit (
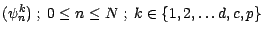 ) la suite vectorielle prévisible à valeurs dans
) la suite vectorielle prévisible à valeurs dans
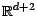 définie par
définie par
D'après la proposition ![[*]](file:/usr/share/latex2html/icons/crossref.gif) , il existe
une statégie autofinancée
, il existe
une statégie autofinancée  coïncidant avec
coïncidant avec 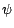 sur les actifs
risqués et telle que
sur les actifs
risqués et telle que
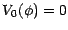 .
.
On a donc
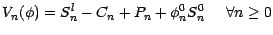
|
(4.16) |
et en particulier,
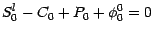 |
(4.17) |
Puisque  est autofinancée, on a d'autre
part
est autofinancée, on a d'autre
part
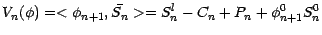
|
(4.18) |
La comparaison de (4.16) et (4.18) montre que
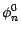 ne
dépend pas de
ne
dépend pas de  ; il résulte alors de
(4.17 ) que
; il résulte alors de
(4.17 ) que
La stratégie  constitue donc un
arbitrage ce qui interdit au marché d'être viable.
constitue donc un
arbitrage ce qui interdit au marché d'être viable.
Dans une salle de marché , la manière pratique de
mettre en oeuvre cette stratégie serait la suivante :
à l'instant 0 vous achetez une action et un put et vous
vendez un call ; cela vous procure une quantité
(algébrique) d'argent liquide égale à
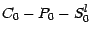 que
vous placez au taux
que
vous placez au taux 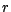 si elle est
si elle est 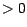 , et que vous empruntez au même taux si elle est
, et que vous empruntez au même taux si elle est
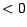 ; vous ne touchez à rien
jusqu'à la date
; vous ne touchez à rien
jusqu'à la date 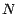 ; votre quantité de
numéraire est alors
; votre quantité de
numéraire est alors
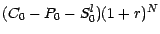 ; deux cas peuvent maintenant se présenter :
; deux cas peuvent maintenant se présenter :
-
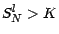 ; l'acheteur du
call l'exerce, vous lui livrez l'action que vous possédez au
prix
; l'acheteur du
call l'exerce, vous lui livrez l'action que vous possédez au
prix 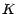 , et votre put ne vaut rien. La valeur de
votre portefeuille est donc bien celle que nous avons
calculée.
, et votre put ne vaut rien. La valeur de
votre portefeuille est donc bien celle que nous avons
calculée.
-
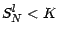 ; l'acheteur du
call a perdu son argent, vous vendez votre action au prix
; l'acheteur du
call a perdu son argent, vous vendez votre action au prix 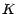 , ce que vous autorise la possession d'un put ; la
valeur de votre portefeuille est encore la même .
, ce que vous autorise la possession d'un put ; la
valeur de votre portefeuille est encore la même .
Vous avez donc réussi à obtenir un "free lunch".
actifs
admettant pour cours à l'instant

et est supposé viable. Nous allons montrer que, si l'égalité (
) n'est pas satisfaite, il existe une stratégie d'arbitrage ; pour ne pas trop alourdir ces notes, nous nous bornerons au cas
en laissant au lecteur, que je sais friand d'exercices, le soin d'en déduire une démonstration générale.
![]() ) la suite vectorielle prévisible à valeurs dans
) la suite vectorielle prévisible à valeurs dans
![]() définie par
définie par
![]() que
vous placez au taux
que
vous placez au taux ![]() si elle est
si elle est ![]() , et que vous empruntez au même taux si elle est
, et que vous empruntez au même taux si elle est
![]() ; vous ne touchez à rien
jusqu'à la date
; vous ne touchez à rien
jusqu'à la date ![]() ; votre quantité de
numéraire est alors
; votre quantité de
numéraire est alors
![]() ; deux cas peuvent maintenant se présenter :
; deux cas peuvent maintenant se présenter :