Il existe une stratégie d'arbitrage  vérifiant
vérifiant
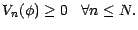 4.1
4.1
Démonstration : Notons d'abord que
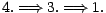 ; on
procède ensuite comme suit :
; on
procède ensuite comme suit :
-
 : Soit
: Soit
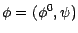 un portefeuille
autofinancé vérifiant (4.11) ; posons
Il résulte des hypothèses faites sur
un portefeuille
autofinancé vérifiant (4.11) ; posons
Il résulte des hypothèses faites sur  que
que
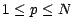 ; d'autre part,
; d'autre part,
 (et en particulier pour
(et en particulier pour 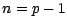 ), on a soit
), on a soit 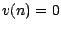 , soit
, soit 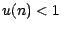 .
.
- Si
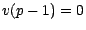 , nous poserons
, nous poserons
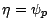 ; on aura alors, puisque
; on aura alors, puisque  est autofinancée,
ce qui entraîne (4.12)
est autofinancée,
ce qui entraîne (4.12)
- Supposons maintenant
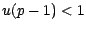 ; nous poserons
alors
; nous poserons
alors
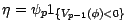 . On peut
alors écrire
ce qui entraîne également (4.12)
. On peut
alors écrire
ce qui entraîne également (4.12)
-
 : Soit
: Soit 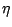 un vecteur aléatoire vérifiant (4.12) ;
définissons la suite prévisible de vecteurs
aléatoires
un vecteur aléatoire vérifiant (4.12) ;
définissons la suite prévisible de vecteurs
aléatoires
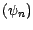 à valeurs dans
à valeurs dans
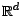 par
et appelons
par
et appelons
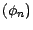 le portefeuille
autofinancé de valeur initiale nulle associé à
le portefeuille
autofinancé de valeur initiale nulle associé à
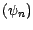 par la proposition 4.2.2 .
On a
si bien que
par la proposition 4.2.2 .
On a
si bien que
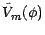 est nul pour
est nul pour 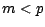 et vaut
et vaut
![$ [\eta , \Delta \tilde{S}_{p}]$](img869.gif) pour
pour 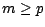 . Le résultat en découle
immédiatement.
. Le résultat en découle
immédiatement.
![]() ; on
procède ensuite comme suit :
; on
procède ensuite comme suit :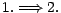 : Soit
: Soit
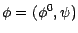 un portefeuille
autofinancé vérifiant (4.11) ; posons
Il résulte des hypothèses faites sur
un portefeuille
autofinancé vérifiant (4.11) ; posons
Il résulte des hypothèses faites sur![$\displaystyle u(n)=\textbf {P}[V_{n}(\phi)\geq 0]\;\;\;;\;\;v(n)=\textbf {P}[V_{n}(\phi)>0]\;\;;\;\;p=\inf\{n\;\vert\;u(n)=1 \;\mathrm{et}\;v(n)>0\}$](img849.gif)
 que
que
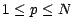 ; d'autre part,
; d'autre part,
 (et en particulier pour
(et en particulier pour 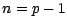 ), on a soit
), on a soit 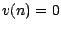 , soit
, soit 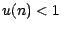 .
.
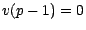 , nous poserons
, nous poserons
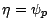 ; on aura alors, puisque
; on aura alors, puisque  est autofinancée,
ce qui entraîne (4.12)
est autofinancée,
ce qui entraîne (4.12)![$\displaystyle [\eta,\Delta \tilde{S}_{p}]=<\phi_{p},\Delta \tilde{S}_{p}>=\tilde{V}_{p}(\phi)-\tilde{V}_{p-1}(\phi)\geq \tilde{V}_{p}(\phi)Â¥$](img857.gif)
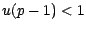 ; nous poserons
alors
; nous poserons
alors
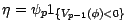 . On peut
alors écrire
ce qui entraîne également (4.12)
. On peut
alors écrire
ce qui entraîne également (4.12)![$\displaystyle [\eta , \Delta \tilde{S}_{p}Â¥]=1_{\{V_{p-1}<0\}}<\phi_{p} , \Del... ...\tilde{V}_{p-1}(\phi)]\geq 1_{\{V_{p-1}<0\}}\big(-\tilde{V}_{p-1}(\phi)\big)Â¥$](img860.gif)
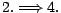 : Soit
: Soit 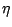 un vecteur aléatoire vérifiant (4.12) ;
définissons la suite prévisible de vecteurs
aléatoires
un vecteur aléatoire vérifiant (4.12) ;
définissons la suite prévisible de vecteurs
aléatoires
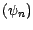 à valeurs dans
à valeurs dans
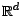 par
et appelons
par
et appelons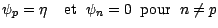
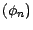 le portefeuille
autofinancé de valeur initiale nulle associé à
le portefeuille
autofinancé de valeur initiale nulle associé à
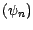 par la proposition 4.2.2 .
On a
si bien que
par la proposition 4.2.2 .
On a
si bien que![$\displaystyle \tilde{V}_{m}(\phi)=\sum_{ 1\leq n \leq m}<\phi_{n},\Delta \tilde{S}_{n}>=\sum_{ 1\leq n\leq m}[\psi_{n},\Delta \tilde{S}_{n}],$](img866.gif)
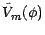 est nul pour
est nul pour 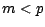 et vaut
et vaut
![$ [\eta , \Delta \tilde{S}_{p}]$](img869.gif) pour
pour 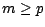 . Le résultat en découle
immédiatement.
. Le résultat en découle
immédiatement.