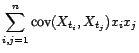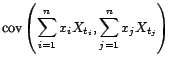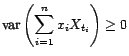Section : Définition et premières propriétés
Précédent : Exercice 7.
Suivant : Caractérisation des processus MA

Preuve de la proposition [*]

  1. C'est une conséquence de l'inégalité de Cauchy-Schwartz :
    $\displaystyle \left\vert {\gamma}_X(h)\right\vert$ $\displaystyle =$ $\displaystyle \left\vert \mathop{\hbox{\upshape {cov}}}\nolimits (X_t,X_{t+h})\right\vert$  
      $\displaystyle =$ $\displaystyle \left\vert {\mathbb{E}}\left[\left(X_t-{\mathbb{E}}\left[X_t\right]\right)\left(X_{t+h}-{\mathbb{E}}\left[X_{t+h}\right]\right)\right]\right\vert$  
      $\displaystyle \leq$ $\displaystyle \sqrt{{\mathbb{E}}\left[\left(X_t-{\mathbb{E}}\left[X_t\right]\ri... ...mathbb{E}}\left[\left(X_{t+h}-{\mathbb{E}}\left[X_{t+h}\right]\right)^2\right]}$  
      $\displaystyle =$ $\displaystyle \sqrt{\mathop{\hbox{\upshape {var}}}\nolimits (X_t)\mathop{\hbox{\upshape {var}}}\nolimits (X_{t+h})}={\gamma}_X(0)$  

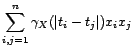    Il en découle la seconde inégalité, car $ {\rho}_X(h)={\gamma}_X(h)/{\gamma}_X(0)$.
  2. C'est une traduction du résultat classique selon lequel les matrices de covariance sont symétriques et positives :
    $\displaystyle \sum_{i,j=1}^n{\gamma}_X(\vert t_i-t_j\vert)x_ix_j$ $\displaystyle =$ $\displaystyle \sum_{i,j=1}^n\mathop{\hbox{\upshape {cov}}}\nolimits (X_{t_i},X_{t_j})x_ix_j$  
      $\displaystyle =$ $\displaystyle \mathop{\hbox{\upshape {cov}}}\nolimits \left(\sum_{i=1}^nx_iX_{t_i},\sum_{j=1}^nx_jX_{t_j}\right)$  
      $\displaystyle =$ $\displaystyle \mathop{\hbox{\upshape {var}}}\nolimits \left(\sum_{i=1}^nx_iX_{t_i}\right)\geq0$  


Thierry Cabanal-Duvillard
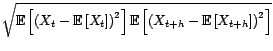
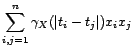