Section : Définition :
Précédent : Définition :
Suivant : Définition :
Soit
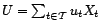 une combinaison
linéaire de
une combinaison
linéaire de
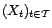 , telle que
, telle que
![$ {\mathbb{E}}_{{\beta},{\sigma}^2}[U]={\mathbb{E}}_{{\beta},{\sigma}^2}[X_s]=f(s,{\beta})$](img372.gif) quel que soit
quel que soit
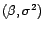 . Alors
. Alors
La variable aléatoire 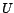 est donc
prédicteur linéaire de
est donc
prédicteur linéaire de 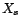 si et
seulement s'il s'agit de l'estimateur de
si et
seulement s'il s'agit de l'estimateur de
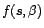 de variance minimale parmi les
estimateurs sans biais linéaires en
de variance minimale parmi les
estimateurs sans biais linéaires en
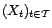 . D'après le
théorème de Gauss-Markov, cet estimateur existe, est
unique, et vaut
. D'après le
théorème de Gauss-Markov, cet estimateur existe, est
unique, et vaut
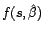 .
.
Soit 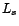 le vecteur ligne tel que
le vecteur ligne tel que
 , et
, et
 la matrice de
covariance de
la matrice de
covariance de
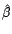 . Si le modèle est
régulier, et peut s'écrire sous la forme
. Si le modèle est
régulier, et peut s'écrire sous la forme
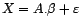 , on rappelle que
, on rappelle que
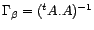 . Alors
l'erreur quadratique moyenne vaut
. Alors
l'erreur quadratique moyenne vaut
On pose
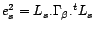 .
.
Thierry Cabanal-Duvillard
![]() le vecteur ligne tel que
le vecteur ligne tel que
![]() , et
, et
![]() la matrice de
covariance de
la matrice de
covariance de
![]() . Si le modèle est
régulier, et peut s'écrire sous la forme
. Si le modèle est
régulier, et peut s'écrire sous la forme
![]() , on rappelle que
, on rappelle que
![]() . Alors
l'erreur quadratique moyenne vaut
. Alors
l'erreur quadratique moyenne vaut