Section : Espaces
de Hilbert
Précédent : Notations.
Suivant : Projecteurs orthogonaux
- Soit
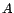 une matrice symétrique
définie positive ; alors
une matrice symétrique
définie positive ; alors
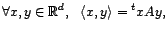 , muni du produit scalaire
est un espace de Hilbert. Si
, muni du produit scalaire
est un espace de Hilbert. Si 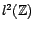 , on retrouve
le produit scalaire canonique.
, on retrouve
le produit scalaire canonique.
- L'espace
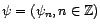 des suites
des suites
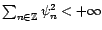 vérifiant
vérifiant
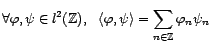 , muni du produit
scalaire
est un espace de Hilbert.
, muni du produit
scalaire
est un espace de Hilbert.
- L'espace
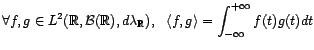 des fonctions réelles de carré intégrable par
rapport à la mesure de Lebesgue, muni du produit scalaire
est un espace de Hilbert. Tout comme l'est plus
généralement l'espace
des fonctions réelles de carré intégrable par
rapport à la mesure de Lebesgue, muni du produit scalaire
est un espace de Hilbert. Tout comme l'est plus
généralement l'espace
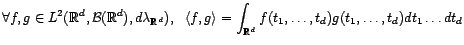 muni du produit scalaire
muni du produit scalaire
- Soit
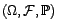 un espace de
probabilité, et
un espace de
probabilité, et
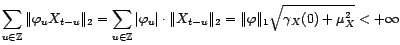 l'ensemble des
variables aléatoires réelles de carré
intégrable. Muni du produit scalaire
c'est un espace de Hilbert.
l'ensemble des
variables aléatoires réelles de carré
intégrable. Muni du produit scalaire
c'est un espace de Hilbert.
- Soient
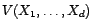 . Le sous-espace
vectoriel
. Le sous-espace
vectoriel
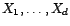 de toutes les
combinaisons linéaires de
de toutes les
combinaisons linéaires de
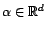 est un espace de Hilbert.
Pour tout
est un espace de Hilbert.
Pour tout
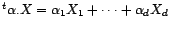 , on note
, on note
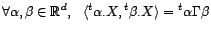 . Alors, si
les variables
. Alors, si
les variables
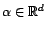 sont centrées,
avec
sont centrées,
avec  la matrice de covariance de
la matrice de covariance de
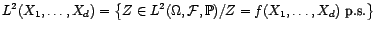 .
.
- Soit
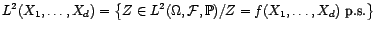 une famille de variables
aléatoires réelles. Alors le sous-espace vectoriel
est un espace de Hilbert.
une famille de variables
aléatoires réelles. Alors le sous-espace vectoriel
est un espace de Hilbert.
- Soit
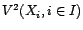 une famille dénombrable
de variables aléatoires de
une famille dénombrable
de variables aléatoires de
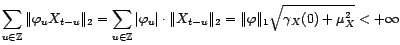 . L'ensemble
. L'ensemble
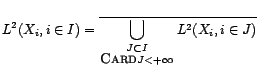 est un espace de
Hilbert.
est un espace de
Hilbert.
- Soit
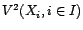 une famille dénombrable
de variables aléatoires réelles. L'espace vectoriel
est un espace de Hilbert.
une famille dénombrable
de variables aléatoires réelles. L'espace vectoriel
est un espace de Hilbert.
Section : Espaces
de Hilbert
Précédent : Notations.
Suivant : Projecteurs orthogonaux
Thierry Cabanal-Duvillard
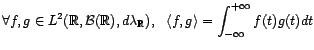 des fonctions réelles de carré intégrable par
rapport à la mesure de Lebesgue, muni du produit scalaire
des fonctions réelles de carré intégrable par
rapport à la mesure de Lebesgue, muni du produit scalaire
 est un espace de
Hilbert.
est un espace de
Hilbert.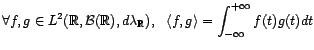 des fonctions réelles de carré intégrable par
rapport à la mesure de Lebesgue, muni du produit scalaire
des fonctions réelles de carré intégrable par
rapport à la mesure de Lebesgue, muni du produit scalaire
 est un espace de
Hilbert.
est un espace de
Hilbert.