Section : Espaces
de Hilbert
Précédent : Espaces de Hilbert
Suivant : Preuve
Soit 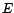 un
un
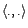 -espace vectoriel.
-espace vectoriel.
- On appelle produit scalaire sur
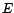 toute
application
toute
application
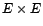 de
de 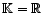 dans
dans
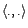 qui soit bilinéaire,
symétrique et définie positive si
qui soit bilinéaire,
symétrique et définie positive si
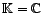 , et
sesquilinéaire, à symétrie hermitienne et
définie positive si
, et
sesquilinéaire, à symétrie hermitienne et
définie positive si
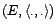 .
.
- Le couple
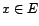 est alors
appelé espace préhilbertien. On définit
alors un norme dite hilbertienne sur
est alors
appelé espace préhilbertien. On définit
alors un norme dite hilbertienne sur 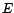 en
posant, pour tout
en
posant, pour tout 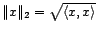 ,
,
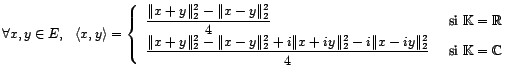 .
Il est équivalent de connaître le produit scalaire ou
la norme hilbertienne, car on a la formule :
.
Il est équivalent de connaître le produit scalaire ou
la norme hilbertienne, car on a la formule :
- Une suite
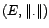 d'éléments d'un espace vectoriel normé
d'éléments d'un espace vectoriel normé
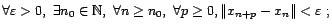 est dite de Cauchy
si
autrement dit, si
est dite de Cauchy
si
autrement dit, si
- Un espace vectoriel normé
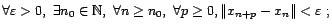 est dit complet si
toute suite de Cauchy d'éléments de
est dit complet si
toute suite de Cauchy d'éléments de 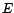 converge dans
converge dans 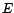 .
.
- L'espace préhilbertien
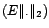 est appelé
espace de Hilbert s'il est complet.
est appelé
espace de Hilbert s'il est complet.
Propriété 5.I.1 Soit
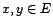 un espace
préhilbertien.
un espace
préhilbertien.
- Inégalité de Cauchy-Schwartz : quels que soient
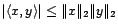 ,
,
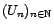 .
.
- Continuité du produit
scalaire : si
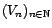 et
et
 sont deux suites
convergentes dans
sont deux suites
convergentes dans 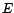 , de limites respectives
, de limites respectives 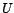 et
et 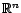 , alors
, alors
Section : Espaces
de Hilbert
Précédent : Espaces de Hilbert
Suivant : Preuve
Thierry Cabanal-Duvillard
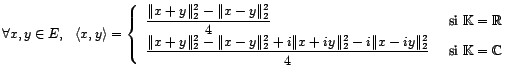 .
Il est équivalent de connaître le produit scalaire ou
la norme hilbertienne, car on a la formule :
.
Il est équivalent de connaître le produit scalaire ou
la norme hilbertienne, car on a la formule :
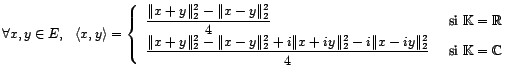 .
Il est équivalent de connaître le produit scalaire ou
la norme hilbertienne, car on a la formule :
.
Il est équivalent de connaître le produit scalaire ou
la norme hilbertienne, car on a la formule :