Section : Prédiction pour un processus
Précédent : Prédiction pour un processus
Suivant : Remarques :
On supposera dans toute la suite les processus ARMA
centrés. En conséquence, on pourra remplacer les
espaces
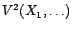 par
par
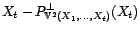 .
.
On pose comme à l'ordinaire
Et on note 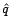 ,
, 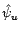 ,
,
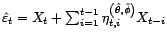 ,
,
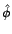 ,
,
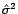 ,
,
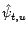 ,
,
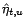 et
et
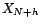 les estimateurs des
différents paramètres du processus. On souhaite
construire un prédicteur de
les estimateurs des
différents paramètres du processus. On souhaite
construire un prédicteur de 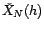 , avec
, avec
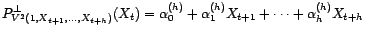 , qu'on notera
, qu'on notera
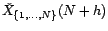 (plutôt que
(plutôt que
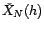 comme précédemment). Comme le processus est
centré, on a
comme précédemment). Comme le processus est
centré, on a
On en déduit le prédicteur linéaire
L'erreur de prédiction vaut
A l'aide de l'inégalité de
BienAymé-Tchebicheff, ou en supposant que le processus soit
gaussien, on peut déduire de ce calcul d'erreur un
intervalle de prévision (approximatif) pour 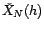 .
.
Section : Prédiction pour un processus
Précédent : Prédiction pour un processus
Suivant : Remarques :
Thierry Cabanal-Duvillard
![]() par
par
![]() .
.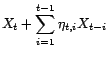
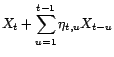
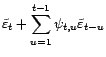
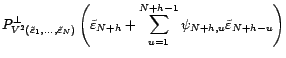
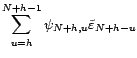
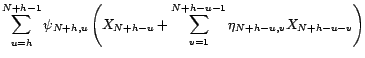
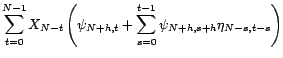

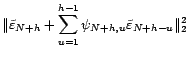
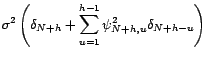
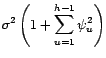
![]() .
.