Section : Prévision
Précédent : Prévision
Suivant : Prédiction pour un processus
Soit
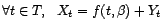 une série temporelle
qu'on modélise par un processus
une série temporelle
qu'on modélise par un processus
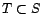 avec
avec
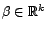 , et de loi
paramètrée par
, et de loi
paramètrée par
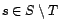 . Soit
. Soit
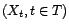 un indice de temps pour
lequel on ne possède pas de relevé. Prédire
un indice de temps pour
lequel on ne possède pas de relevé. Prédire
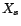 , c'est déterminer une variable
aléatoire fonction de
, c'est déterminer une variable
aléatoire fonction de
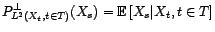 la plus proche possible de
la plus proche possible de
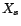 . Si l'on mesure la distance entre deux
variables par la norme hilbertienne, alors le meilleur
prédicteur au sens des moindres carrés est
. Si l'on mesure la distance entre deux
variables par la norme hilbertienne, alors le meilleur
prédicteur au sens des moindres carrés est
Cette fonction n'est pas en général calculable (sauf
dans le cas gaussien), et l'on préfère se limiter aux
fonctions affines de
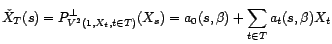 . On parle alors de
meilleur prédicteur affine au sens des moindres
carrés. Il s'agit de
Rappelons que dans le cas d'un processus gaussien on a
l'égalité entre
. On parle alors de
meilleur prédicteur affine au sens des moindres
carrés. Il s'agit de
Rappelons que dans le cas d'un processus gaussien on a
l'égalité entre
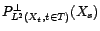 et
et
 .
.
Les coefficients 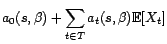 sont
caractérisés par le système
d'équations
sont
caractérisés par le système
d'équations
Le problème évident est que la variable
aléatoire
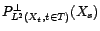 dépend du paramètre
dépend du paramètre 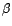 en
général inconnu, qu'on est donc amené à
remplacer par son estimateur
en
général inconnu, qu'on est donc amené à
remplacer par son estimateur
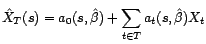 . On obtient
ainsi le prédicteur
L'erreur quadratique commise vaut alors
Le premier terme
. On obtient
ainsi le prédicteur
L'erreur quadratique commise vaut alors
Le premier terme
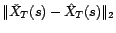 correspond
à l'erreur de prédiction pure, le second
correspond
à l'erreur de prédiction pure, le second
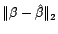 à l'erreur d'estimation. Il est difficile de calculer
exactement l'erreur totale, ni même l'erreur d'estimation,
sauf dans le cas des modèles linéaires. L'erreur de
prédiction pure est en revanche plus simple à
déterminer. C'est aussi en général le terme
dominant : en effet, les différents résultats de
convergence montrent le plus souvent que
à l'erreur d'estimation. Il est difficile de calculer
exactement l'erreur totale, ni même l'erreur d'estimation,
sauf dans le cas des modèles linéaires. L'erreur de
prédiction pure est en revanche plus simple à
déterminer. C'est aussi en général le terme
dominant : en effet, les différents résultats de
convergence montrent le plus souvent que
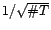 est de
l'ordre de
est de
l'ordre de
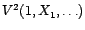 , dont il suit, par
continuité, qu'il en est de même pour l'erreur
d'estimation. Comme nous le verrons, il n'en est pas de même
pour l'erreur de prédiction pure, que dans la pratique on
est amené à confondre avec l'erreur totale commise.
, dont il suit, par
continuité, qu'il en est de même pour l'erreur
d'estimation. Comme nous le verrons, il n'en est pas de même
pour l'erreur de prédiction pure, que dans la pratique on
est amené à confondre avec l'erreur totale commise.
Section : Prévision
Précédent : Prévision
Suivant : Prédiction pour un processus
Thierry Cabanal-Duvillard
![]() une série temporelle
qu'on modélise par un processus
une série temporelle
qu'on modélise par un processus
![]() avec
avec
![]() , et de loi
paramètrée par
, et de loi
paramètrée par
![]() . Soit
. Soit
![]() un indice de temps pour
lequel on ne possède pas de relevé. Prédire
un indice de temps pour
lequel on ne possède pas de relevé. Prédire
![]() , c'est déterminer une variable
aléatoire fonction de
, c'est déterminer une variable
aléatoire fonction de
![]() la plus proche possible de
la plus proche possible de
![]() . Si l'on mesure la distance entre deux
variables par la norme hilbertienne, alors le meilleur
prédicteur au sens des moindres carrés est
. Si l'on mesure la distance entre deux
variables par la norme hilbertienne, alors le meilleur
prédicteur au sens des moindres carrés est
![]() sont
caractérisés par le système
d'équations
sont
caractérisés par le système
d'équations