Section : Choix
d'un modèle et
Précédent : Choix d'un modèle et
Suivant : Remarques :
Soient 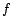 et
et 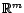 deux
densités de probabilité sur
deux
densités de probabilité sur
 . On appelle information
de Kullback de
. On appelle information
de Kullback de 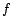 par rapport à
par rapport à 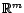 la valeur suivante :
la valeur suivante :
Propriété 3.V.1
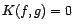 est positive.
est positive.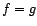 si et seulement si
si et seulement si 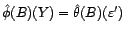 .
.
Soit
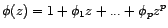 une réalisation d'un
processus
une réalisation d'un
processus  ARMA(
ARMA(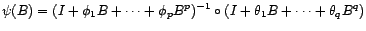 ) gaussien,
vérifiant
) gaussien,
vérifiant
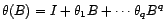 , et
on note
, et
on note
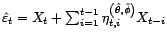 ,
,
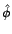 et
et
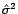 les estimateurs du maximum de
vraisemblance (on suppose correctement estimés
les estimateurs du maximum de
vraisemblance (on suppose correctement estimés  et
et 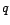 ). Soit
). Soit 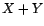 le processus
ARMA vérifiant
le processus
ARMA vérifiant
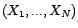 , avec
, avec
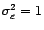 bruit blanc de variance
bruit blanc de variance
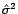 .
.
La densité de probabilité du vecteur
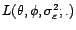 est donnée par
est donnée par
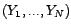 tandis que
celle de
tandis que
celle de
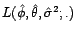 est donnée par
est donnée par
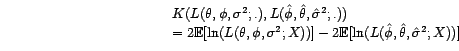 . La distance de
Kullback entre le modèle exact et le modèle
estimé vaut donc
. La distance de
Kullback entre le modèle exact et le modèle
estimé vaut donc
Minimiser cette distance revient à minimiser
Or on a l'estimation
Akaïke a donc proposé de choisir comme modèle
celui qui minimise
Ce critère a tendance à conduire à une
surestimation des valeurs de  et
et 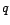 .
Akaïke en a donc proposé une modification, le
critère bayésien de Schwartz :
Les estimateurs de
.
Akaïke en a donc proposé une modification, le
critère bayésien de Schwartz :
Les estimateurs de  et
et 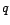 obtenus
par minimisation de ce critère ont le mérite
d'être convergents.
obtenus
par minimisation de ce critère ont le mérite
d'être convergents.
Section : Choix
d'un modèle et
Précédent : Choix d'un modèle et
Suivant : Remarques :
Thierry Cabanal-Duvillard
 . On appelle information
de Kullback de
. On appelle information
de Kullback de ![]() une réalisation d'un
processus
une réalisation d'un
processus ![]() ARMA(
ARMA(![]() ) gaussien,
vérifiant
) gaussien,
vérifiant
![]() , et
on note
, et
on note
![]() ,
,
![]() et
et
![]() les estimateurs du maximum de
vraisemblance (on suppose correctement estimés
les estimateurs du maximum de
vraisemblance (on suppose correctement estimés ![]() et
et ![]() ). Soit
). Soit ![]() le processus
ARMA vérifiant
le processus
ARMA vérifiant
![]() , avec
, avec
![]() bruit blanc de variance
bruit blanc de variance
![]() .
.![]() est donnée par
est donnée par
![]() tandis que
celle de
tandis que
celle de
![]() est donnée par
est donnée par
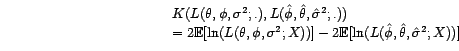 . La distance de
Kullback entre le modèle exact et le modèle
estimé vaut donc
. La distance de
Kullback entre le modèle exact et le modèle
estimé vaut donc
![\begin{displaymath} \begin{array}{l} K(L({\theta},{\phi},{\sigma^2};.),L(\hat{\p... ...}[\ln(L(\hat{\phi},\hat{\theta},\hat{\sigma}^2;X))] \end{array}\end{displaymath}](img1405.gif)
![\begin{displaymath} \begin{array}{l} -2{\mathbb{E}}\Bigl[\ln\bigl(L(\hat{\phi},\... ... {{\delta}_t^{(\hat{\theta},\hat{\phi})}}\right] -N \end{array}\end{displaymath}](img1406.gif)