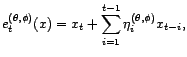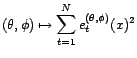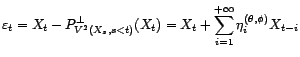 . L'erreur de
prédiction à l'instant
. L'erreur de
prédiction à l'instant
Les deux méthodes, des moindres carrés ordinaires
et du maximum de vraisemblance, sont comme ont l'a vu très
proches l'une de l'autre. Elles le sont en particulier en ceci
qu'elles nécessitent à chaque évaluation de la
fonction à minimiser le calcul de ![]() coefficients obtenus par l'algorithme des innovations (ce nombre
peut néanmoins être bien plus faible dans le cas d'un
processus ARMA - voir exercices). Cette complexité peut
devenir problématique, notamment pour de grands
échantillons. La méthode des moindres carrés
conditionnels s'avère alors plus adaptée. Elle est
assez similaire aux précédentes, car elle consiste
aussi à minimiser les erreurs de prédiction, mais en
supposant qu'avant l'instant initial les valeurs inconnues prises
par la série
coefficients obtenus par l'algorithme des innovations (ce nombre
peut néanmoins être bien plus faible dans le cas d'un
processus ARMA - voir exercices). Cette complexité peut
devenir problématique, notamment pour de grands
échantillons. La méthode des moindres carrés
conditionnels s'avère alors plus adaptée. Elle est
assez similaire aux précédentes, car elle consiste
aussi à minimiser les erreurs de prédiction, mais en
supposant qu'avant l'instant initial les valeurs inconnues prises
par la série ![]() sont nulles, c-à-d
en conditionnant par
sont nulles, c-à-d
en conditionnant par
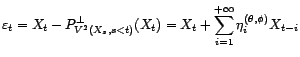 . L'erreur de
prédiction à l'instant
. L'erreur de
prédiction à l'instant ![]() sachant tout
le passé n'est autre que l'innovation :
sachant tout
le passé n'est autre que l'innovation :
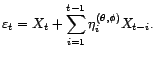
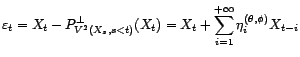 , on a
, on a