Section : Estimation préliminaire
Précédent : Estimation de la partie
Suivant : Estimateurs des moindres carrés
On s'appuie sur la remarque simple suivante :
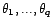 est un processus MA(
est un processus MA(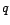 ), de paramètres
), de paramètres
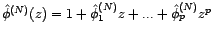 .
.
Une fois calculé
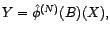 , on pose
, on pose
et l'on détermine les estimateurs
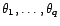 de
de
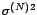 en appliquant
à
en appliquant
à 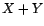 l'algorithme des innovations. On en
déduit également l'estimateur
l'algorithme des innovations. On en
déduit également l'estimateur
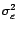 de la variance du bruit
blanc
de la variance du bruit
blanc
 .
.
Thierry Cabanal-Duvillard
![]() est un processus MA(
est un processus MA(![]() ), de paramètres
), de paramètres
![]() .
.![]() , on pose
, on pose