Section : Estimation préliminaire
Précédent : Estimation préliminaire
Suivant : Estimation de la partie
Si  est un processus ARMA
est un processus ARMA causal et inversible, vérifiant
causal et inversible, vérifiant
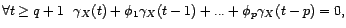 alors on a vu que sa fonction d'autocovariance vérifie la
relation de récurrence suivante :
et que l'on peut en déduire le système
d'équations dit aussi de Yule-Walker
Les estimateurs de Yule-Walker de
alors on a vu que sa fonction d'autocovariance vérifie la
relation de récurrence suivante :
et que l'on peut en déduire le système
d'équations dit aussi de Yule-Walker
Les estimateurs de Yule-Walker de
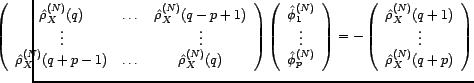 sont donc
naturellement définis par
sont donc
naturellement définis par
Thierry Cabanal-Duvillard
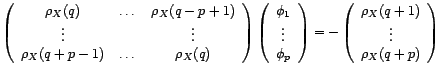
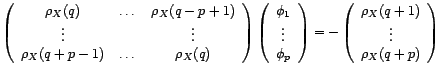
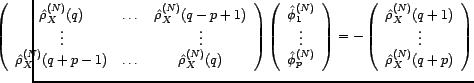 sont donc
naturellement définis par
sont donc
naturellement définis par