Section : Décomposition de Wold
Précédent : Décomposition de Wold
Suivant : Remarque :
- Un processus du second ordre
 est dit
déterministe ou singulier s'il vérifie
autrement dit, si
Il est dit régulier si
est dit
déterministe ou singulier s'il vérifie
autrement dit, si
Il est dit régulier si
Théorème 2.IV.1 Soit
 un processus
faiblement stationnaire centré. Alors il existe, et de
façon unique, une suite réelle
un processus
faiblement stationnaire centré. Alors il existe, et de
façon unique, une suite réelle
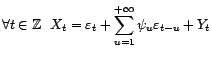 , un bruit blanc faible
, un bruit blanc faible
 , et un processus
déterministe
, et un processus
déterministe  tels que
la série convergeant pour la norme hilbertienne. De
plus
tels que
la série convergeant pour la norme hilbertienne. De
plus
-
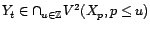 .
.
-
 est le bruit blanc d'innovation
associé à
est le bruit blanc d'innovation
associé à  .
.
- quel que soit
 ,
,
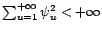 .
.
-
 et
et  sont
décorrélés.
sont
décorrélés.
-
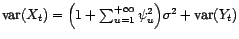 et
et
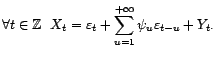 avec
avec
 la variance de
la variance de
 .
.
Thierry Cabanal-Duvillard
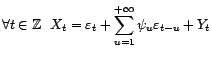 , un bruit blanc faible
, un bruit blanc faible
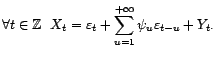 avec
avec