Section : Représentation causale et inversible
Précédent : Exercice 22.
Suivant : Exercice 24.
Soit
 un processus du
second ordre, faiblement stationnaire de type AR(1) :
avec
un processus du
second ordre, faiblement stationnaire de type AR(1) :
avec
 bruit blanc de variance
bruit blanc de variance
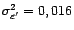 . Soit
. Soit
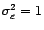 un bruit blanc de variance
un bruit blanc de variance
 ,
indépendant de
,
indépendant de
 .
.
- Montrer que le processus
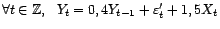 est faiblement stationnaire. En déduire qu'il existe une
solution
est faiblement stationnaire. En déduire qu'il existe une
solution 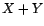 faiblement stationnaire à
l'équation
faiblement stationnaire à
l'équation
- Montrer que
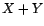 est un ARMA(2,1) (Indication : on
pourra raisonner en se servant de la densité spectrale, ou
en considérant le processus
est un ARMA(2,1) (Indication : on
pourra raisonner en se servant de la densité spectrale, ou
en considérant le processus
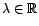 ).
).
- Donner de
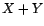 une représentation MA(
une représentation MA(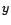 ), déterminée à partir de sa
représentation causale et inversible, et préciser le
calcul du bruit blanc d'innovation associé à
), déterminée à partir de sa
représentation causale et inversible, et préciser le
calcul du bruit blanc d'innovation associé à 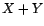 en fonction de
en fonction de
 et
et
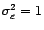 .
.
Thierry Cabanal-Duvillard