Section : Représentation causale et inversible
Précédent : Exercice 21.
Suivant : Exercice 23.
Soient  et
et 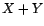 les processus
définis par
les processus
définis par
avec
 et
et
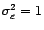 deux bruits blancs de
variances
deux bruits blancs de
variances
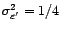 et
et
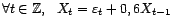 .
.
- De quel type de processus ARMA s'agit-il ? Préciser pour
chacun si le modèle qui le définit est causal ou
inversible.
- Calculer et comparer les fonctions d'autocovariance de
 et
et 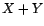 . Expliquer.
. Expliquer.
Thierry Cabanal-Duvillard