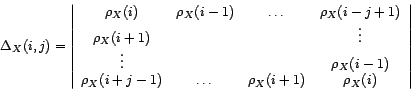Section : Représentation causale et inversible
Précédent : Remarque :
Suivant : Exercice 21.
Soit
 un processus
faiblement stationnaire. On dit qu'il s'agit d'un processus ARMA
décentré si
un processus
faiblement stationnaire. On dit qu'il s'agit d'un processus ARMA
décentré si 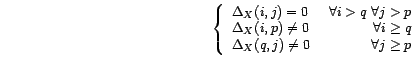 est un
processus ARMA.
est un
processus ARMA.
Il existe aussi, pour les processus ARMA(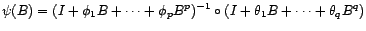 ) des caractérisations analogues à celles
qui ont été établies pour les processus
AR(
) des caractérisations analogues à celles
qui ont été établies pour les processus
AR( ) et MA(
) et MA(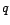 ). On admettra
celle-ci :
). On admettra
celle-ci :
Théorème 2.III.10
(Méthode du coin) Soit  un processus
faiblement stationnaire dont la fonction d'autocorrélation
tend vers 0 en l'infini. C'est un ARMA(
un processus
faiblement stationnaire dont la fonction d'autocorrélation
tend vers 0 en l'infini. C'est un ARMA(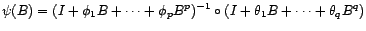 ) -
centré ou non - si et seulement si
avec
) -
centré ou non - si et seulement si
avec
Thierry Cabanal-Duvillard
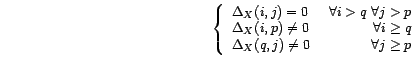 est un
processus ARMA.
est un
processus ARMA.
![]() ) des caractérisations analogues à celles
qui ont été établies pour les processus
AR(
) des caractérisations analogues à celles
qui ont été établies pour les processus
AR(![]() ) et MA(
) et MA(![]() ). On admettra
celle-ci :
). On admettra
celle-ci :