Section : Représentation causale et inversible
Précédent : Démonstration
Suivant : Définition :
Cela implique notamment que tout processus ARMA est centré.
En effet, si
 est un processus
faiblement stationnaire vérifiant
est un processus
faiblement stationnaire vérifiant
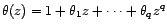 ,
alors
Comme
,
alors
Comme 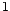 n'est pas racine de
n'est pas racine de
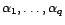 , cela montre que
, cela montre que  .
.
Thierry Cabanal-Duvillard