Section : Décomposition de Doob d'une
Précédent : Décomposition de Doob d'une
Suivant : Un
deuxième temps d'arrêt
Soit (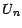 ) une surmartingale ; il existe une
martingale (
) une surmartingale ; il existe une
martingale (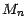 ) et une suite croissante
prévisible
) et une suite croissante
prévisible
((
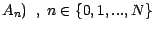 )) telles
que
)) telles
que 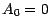 et
et
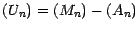 |
(3.9) |
Une telle décomposition ( appelée
décomposition de Doob) est unique .
Démonstration : Pour établir
l'unicité , montrons que la décomposition 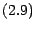 détermine complètement (
détermine complètement (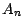 ) , (et par conséquent (
) , (et par conséquent (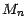 ) ) ;
à l'origine , tout est facile :
) ) ;
à l'origine , tout est facile : 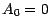 et
et 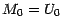 , si bien qu'il suffit de déterminer les
accroissements de (
, si bien qu'il suffit de déterminer les
accroissements de (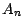 ) ; or , en conditionnant
les 2 membres des égalités
) ; or , en conditionnant
les 2 membres des égalités
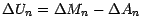 par
par
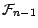 , on obtient pour
, on obtient pour 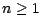
![$\displaystyle \Delta A_n=-\textbf{E}[\Delta U_n\vert {\cal F}_{n-1}]$](img753.gif)
|
(3.10) |
d'où l'unicité ; l'existence se prouve en
définissant 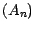 par la formule
par la formule 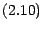 ; la suite ainsi construite est manifestement
prévisible ; de plus ,
; la suite ainsi construite est manifestement
prévisible ; de plus ,
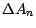 est
est 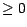 puisque
puisque
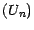 est une surmartingale ;
est une surmartingale ; 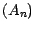 est donc une suite croissante . Il nous reste à
montrer que la suite
est donc une suite croissante . Il nous reste à
montrer que la suite 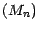 définie par
définie par
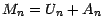 est une martingale ;
écrivons pour cela
est une martingale ;
écrivons pour cela
![$ \Delta M_n=\Delta U_n-\textbf{E}[\Delta U_n\vert {\cal F}_{n-1}]$](img758.gif) et conditionnons les 2 membres : il vient
et conditionnons les 2 membres : il vient
![$ \textbf{E}[\Delta M_n\vert {\cal F}_{n-1}]=0$](img759.gif) ,
C.Q.F.D.
,
C.Q.F.D.
Section : Décomposition de Doob d'une
Précédent : Décomposition de Doob d'une
Suivant : Un
deuxième temps d'arrêt
Jacques Azéma
détermine complètement (
) , (et par conséquent (
) ) ; à l'origine , tout est facile :
et
, si bien qu'il suffit de déterminer les accroissements de (
) ; or , en conditionnant les 2 membres des égalités
par
, on obtient pour
par la formule
; la suite ainsi construite est manifestement prévisible ; de plus ,
est
puisque
est une surmartingale ;
est donc une suite croissante . Il nous reste à montrer que la suite
définie par
est une martingale ; écrivons pour cela
et conditionnons les 2 membres : il vient
, C.Q.F.D.